If the Underlying Populations Cannot Be Assumed to Be Normal,then

Multiple Choice

If the underlying populations cannot be assumed to be normal,then by the central limit theorem,the sampling distribution of 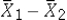is approximately normal only if both sample sizes are sufficiently large-that is,when _________ .

A) n₁ + n₂ = 30
B) n₁ + n₂ ≥ 30
C) n₁ = 30 and n₂ = 30
D) n₁ ≥ 30 and n₂ ≥ 30