The Following Regression Model Was Estimated to Forecast the Percentage $\mu$

Multiple Choice

The following regression model was estimated to forecast the percentage change in the Australian Dollar (AUD) : AUD_t = a₀ + a₁INT_t + a₂INF_{t - 1} + $\mu$ _t,
Where AUD is the quarterly change in the Australian Dollar, INT is the real interest rate differential in period t between the U.S. and Australia, and INF is the inflation rate differential between the U.S. and Australia in the previous period. Regression results indicate coefficients of a₀ = .001; a₁ = -.8; and a₂ = .5. Assume that INF_{t - 1} = 4%. However, the interest rate differential is not known at the beginning of period t and must be estimated. You have developed the following probability distribution: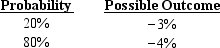
There is a 20% probability that the Australian dollar will change by ____, and an 80% probability it will change by ____.

A) 4.5%; 6.1%;
B) 6.1%; 4.5%
C) 4.5%; 5.3%
D) None of the above