You Have Collected Data from Major League Baseball (MLB)to Find

Essay

You have collected data from Major League Baseball (MLB)to find the determinants of winning.You have a general idea that both good pitching and strong hitting are needed to do well.However,you do not know how much each of these contributes separately.To investigate this problem,you collect data for all MLB during 1999 season.Your strategy is to first regress the winning percentage on pitching quality ("Team ERA"),second to regress the same variable on some measure of hitting ("OPS - On-base Plus Slugging percentage"),and third to regress the winning percentage on both.
Summary of the Distribution of Winning Percentage,On Base plus Slugging Percentage,
and Team Earned Run Average for MLB in 1999
The results are as follows: 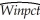= 0.94 - 0.100 × teamera, 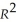= 0.49,SER = 0.06. 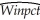= -0.68 + 1.513 × ops, 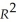=0.45,SER = 0.06. 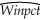= -0.19 - 0.099 × teamera + 1.490 × ops, 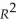=0.92,SER = 0.02.
(a)Interpret the multiple regression.What is the effect of a one point increase in team ERA? Given that the Atlanta Braves had the most wins that year,wining 103 games out of 162,do you find this effect important? Next analyze the importance and statistical significance for the OPS coefficient.(The Minnesota Twins had the minimum OPS of 0.712,while the Texas Rangers had the maximum with 0.840. )Since the intercept is negative,and since winning percentages must lie between zero and one,should you rerun the regression through the origin?
(b)What are some of the omitted variables in your analysis? Are they likely to affect the coefficient on Team ERA and OPS given the size of the 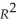and their potential correlation with the included variables?