Solved

The Large-Sample Distribution of 1 Is

Question 3

Multiple Choice

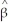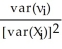The large-sample distribution of The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 1 is


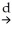A) The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 (
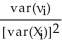The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 1-β1)
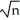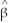The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 N(0
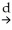The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 where νi= (Xi-μx) ui
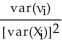B) The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 (
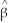The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 1-β1)
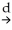The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 N(0
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 where νi= ui
C) The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 (
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 1-β1)
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 N(0
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 where νi= Xiui
D) The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 (
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 1-β1)
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0 N(0
The large-sample distribution of 1 is A) ( 1-β1) N(0 where νi= (Xi-μx) ui B) ( 1-β1) N(0 where νi= ui C) ( 1-β1) N(0 where νi= Xiui D) ( 1-β1) N(0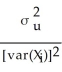

Correct Answer:

verifed

Verified

Related Questions

Q1: It is possible for an estimator of

Q2: E <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="E A)is

Q2: If the errors are heteroskedastic, then<br>A)the OLS

Q5: Finite-sample distributions of the OLS estimator and

Q6: Assume that var(ui|Xi)= θ0+θ1 <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB2833/.jpg" alt="Assume

Q10: Under the five extended least squares assumptions,the

Q12: Feasible WLS does not rely on the

Q17: Asymptotic distribution theory is<br>A)not practically relevant, because

Q23: Discuss the properties of the OLS estimator

Q33: When the errors are heteroskedastic, then<br>A)WLS is