Essay
Consider the following model Yt = β0 + 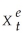 + ut where the superscript "e" indicates expected values.This may represent an example where consumption depends on expected,or "permanent," income.Furthermore,let expected income be formed as follows:
+ ut where the superscript "e" indicates expected values.This may represent an example where consumption depends on expected,or "permanent," income.Furthermore,let expected income be formed as follows: 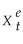 =
= 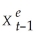 + λ(Xt -
+ λ(Xt - 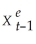 );0 < λ < 1
);0 < λ < 1
(a)In the above expectation formation hypothesis,expectations are formed at the end of the period,say the 31st of December,if you had annual data.Give an intuitive explanation for this process.
(b)Rewrite the expectations equation in the following form: 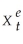 = (1 - λ)
= (1 - λ) 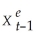 + λXt
+ λXt
Next,following the method used in your textbook,lag both sides of the equation and replace 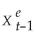 .Repeat this process by repeatedly substituting expression for
.Repeat this process by repeatedly substituting expression for 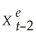 ,
, 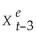 ,and so forth.Show that this results in the following equation:
,and so forth.Show that this results in the following equation: 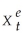 = λXt + λ(1-λ)Xt-1 + λ(1- λ)2 Xt-2 + ...+ λ(1- λ)n Xt-n + (1 - λ)n+1
= λXt + λ(1-λ)Xt-1 + λ(1- λ)2 Xt-2 + ...+ λ(1- λ)n Xt-n + (1 - λ)n+1 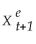 Explain why it is reasonable to drop the last right hand side term as n becomes large.
Explain why it is reasonable to drop the last right hand side term as n becomes large.
(c)Substitute the above expression into the original model that related Y to 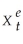 .Although you now have right hand side variables that are all observable,what do you perceive as a potential problem here if you wanted to estimate this distributed lag model without further restrictions?
.Although you now have right hand side variables that are all observable,what do you perceive as a potential problem here if you wanted to estimate this distributed lag model without further restrictions?
(d)Lag both sides of the equation,multiply through by (1- λ),and subtract this equation from the equation found in (c).This is called a "Koyck transformation." What does the resulting equation look like? What is the error process? What is the impact effect (zero-period dynamic multiplier)of a unit change in X,and how does it differ from long run cumulative dynamic multiplier?
Correct Answer:

Verified
(a)If the forecast error for the previou...View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Correct Answer:
Verified
View Answer
Unlock this answer now
Get Access to more Verified Answers free of charge
Q2: Your textbook mentions heteroskedasticity- and autocorrelation- consistent
Q23: The Gallup Poll frequently surveys the electorate
Q24: In your intermediate macroeconomics course,government expenditures and
Q25: The distributed lag model assumptions include all
Q27: (Requires some calculus)In the following,assume that Xt
Q27: In the distributed lag model, the dynamic
Q29: Consider the distributed lag model Yt =
Q32: It has been argued that Canada's aggregate
Q40: In the distributed lag model, the coefficient
Q46: GLS involves<br>A)writing the model in differences and