Solved

Consider the Standard AR(1)Yt = β0 + β1Yt-1 + Ut,where

Question 21

Essay

Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold.
(a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0.
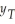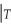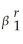
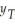(b)Show that the r-period ahead forecast E( Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . 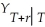+r Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . )= Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . for large r?
(c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . +r Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . )= 0.5 Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r 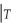)= 0.5 .Show that in the present case this is given by r = - . .Show that in the present case this is given by r = - Consider the standard AR(1)Yt = β0 + β1Yt-1 + ut,where the usual assumptions hold. (a)Show that yt = β0Yt-1 + ut,where yt is Yt with the mean removed,i.e. ,yt = Yt - E(Yt).Show that E(Yt)= 0. (b)Show that the r-period ahead forecast E( +r )= .If 0 < β1 < 1,how does the r-period ahead forecast behave as r becomes large? What is the forecast of for large r? (c)The median lag is the number of periods it takes a time series with zero mean to halve its current value (in expectation),i.e. ,the solution r to E( +r )= 0.5 .Show that in the present case this is given by r = - . .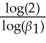

Correct Answer:

verifed

Verified

(a)E(YT)= blured image + β1E(Yt-1),since E(ut)= 0.Th...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q1: To choose the number of lags in

Q3: Autoregressive distributed lag models include<br>A)current and lagged

Q15: One reason for computing the logarithms (ln),

Q16: Consider the AR(1)model Yt = β0 +

Q18: The ADL(p,q)model is represented by the following

Q23: If a "break" occurs in the population

Q24: You collect monthly data on the money

Q27: The random walk model is an example

Q32: The BIC is a statistic<br>A)commonly used to

Q34: The Augmented Dickey Fuller (ADF)t-statistic<br>A)has a normal