Consider the Following Model

Essay

Consider the following model
Yt = α0 + α1 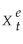+ ut
where the superscript "e" indicates expected values.This may represent an example where consumption depended on expected,or "permanent," income.Furthermore,let expected income be formed as follows: 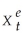= 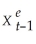+ λ(Xt-1 - );0 < λ < 1
This particular type of expectation formation is called the "adaptive expectations hypothesis."
(a)In the above expectation formation hypothesis,expectations are formed at the beginning of the period,say the 1st of January if you had annual data.Give an intuitive explanation for this process.
(b)Transform the adaptive expectation hypothesis in such a way that the right hand side of the equation only contains observable variables,i.e. ,no expectations.
(c)Show that by substituting the resulting equation from the previous question into the original equation,you get an ADL(0,∞)type equation.How are the coefficients of the regressors related to each other?
(d)Can you think of a transformation of the ADL(0,∞)equation into an ADL(1,1)type equation,if you allowed the error term to be (ut - λut-1)?