Solved

Assume That the Population Distributions of Times (In Hours) of Two

Question 2

Essay

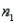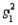Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. = 10, = 2.5, = 0.04 = 11, = 2.6, = 0.09 Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries. 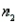= 10, Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. = 10, = 2.5, = 0.04 = 11, = 2.6, = 0.09 Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries. 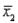= 2.5, Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. = 10, = 2.5, = 0.04 = 11, = 2.6, = 0.09 Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries. 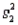= 0.04 Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. = 10, = 2.5, = 0.04 = 11, = 2.6, = 0.09 Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries. = 11, Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. = 10, = 2.5, = 0.04 = 11, = 2.6, = 0.09 Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries. = 2.6, Assume that the population distributions of times (in hours) of two different surgeries are normal with equal variances. Two random samples, drawn independently from the populations, showed the following statistics. = 10, = 2.5, = 0.04 = 11, = 2.6, = 0.09 Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries. = 0.09
Construct and interpret a 90% confidence interval for the true difference in mean amount of time of the two surgeries.

Correct Answer:

verifed

Verified

Related Questions

Q1: A researcher believes she has designed

Q3: Snowmobile Speeds Narrative<br>A customer was interested in

Q4: Motorcycle Fuel Consumption Narrative<br>A Harley Davidson dealer

Q5: Bottling Productivity Narrative<br>Five soft drink bottling companies

Q6: Disinfectant Experiments Narrative<br>An experiment to determine the

Q7: Running Shoes Narrative<br>A new runner has decided

Q8: Snowmobile Speeds Narrative<br>A customer was interested in

Q9: Manufacturing Garment Average Narrative<br>A garment manufacturing company

Q10: Given a random variable that has a

Q11: Average Telephone Time on Hold Narrative<br>A customer