Solved

If X Is a Normal Random Variable with Mean

Question 66

True/False

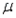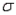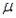If x is a normal random variable with mean If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 4 and standard deviation If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). 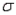= 2, and Y is a normal random variable with mean If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 10 and standard deviation If x is a normal random variable with mean = 4 and standard deviation = 2, and Y is a normal random variable with mean = 10 and standard deviation = 5, then P(x < 0) = P(Y < 0). = 5, then P(x < 0) = P(Y < 0).

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q61: Annual Rainfall Narrative<br>The annual rainfall in a

Q62: A television set manufacturer has found the

Q63: For a continuous random variable x, P(6

Q64: Salmon Flies Lifespan<br>The lifetime of salmon flies

Q67: A normal random variable x has an

Q68: Suppose z has a standard normal distribution.

Q69: A chemical manufacturer sells its product in

Q70: The probability density function of a uniform

Q71: National Achievement Test Scores Narrative<br>The scores on

Q73: The scores on an aptitude test are