Solved

Solution Volumes an Analytical Chemist Wanted to Use Electrolysis to Determine the Determine

Question 63

Essay

Solution Volumes
An analytical chemist wanted to use electrolysis to determine the number of moles of cupric ions in a given volume of solution. The solution was partitioned into n = 30 portions of 0.2 mL each. Each of the n = 30 portions was tested. The average number of moles of cupric ions for the n = 30 portions was found to be 0.185 mole; the standard deviation was 0.015 mole.
-Refer to the Solution Volumes statement. Calculate the intervals ( Solution Volumes An analytical chemist wanted to use electrolysis to determine the number of moles of cupric ions in a given volume of solution. The solution was partitioned into n = 30 portions of 0.2 mL each. Each of the n = 30 portions was tested. The average number of moles of cupric ions for the n = 30 portions was found to be 0.185 mole; the standard deviation was 0.015 mole. -Refer to the Solution Volumes statement. Calculate the intervals ( ), ( ), and ( ). ), ( Solution Volumes An analytical chemist wanted to use electrolysis to determine the number of moles of cupric ions in a given volume of solution. The solution was partitioned into n = 30 portions of 0.2 mL each. Each of the n = 30 portions was tested. The average number of moles of cupric ions for the n = 30 portions was found to be 0.185 mole; the standard deviation was 0.015 mole. -Refer to the Solution Volumes statement. Calculate the intervals ( ), ( ), and ( ). ), and ( Solution Volumes An analytical chemist wanted to use electrolysis to determine the number of moles of cupric ions in a given volume of solution. The solution was partitioned into n = 30 portions of 0.2 mL each. Each of the n = 30 portions was tested. The average number of moles of cupric ions for the n = 30 portions was found to be 0.185 mole; the standard deviation was 0.015 mole. -Refer to the Solution Volumes statement. Calculate the intervals ( 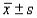), ( ), 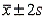and ( ). ).

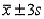Correct Answer:

verifed

Verified

( blured image ) = 0.185 blured image 0.015 or 0.170 t...

View Answer

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q58: If a distribution is strongly skewed by

Q59: Tchebysheff's Theorem states the following: Given a

Q60: Aptitude Tests<br>Twenty-eight applicants interested in working in

Q61: Ice Cream Cone Sales<br>A neighbourhood ice cream

Q62: Amount of Food Sold<br>Suppose the hourly dollar

Q64: The mode is the sum of a

Q65: Which of the following randomly selected measurements,

Q66: Aptitude Tests<br>Twenty-eight applicants interested in working in

Q67: In assembling a home appliance, workers generally

Q68: A sample of 600 values produced the