Exhibit: Consumption, Income, and Wealth Over the Life Cycle $T$ Years and Work

Essay

Exhibit: Consumption, Income, and Wealth Over the Life Cycle 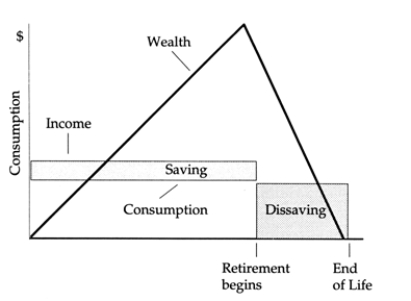Consider the stylized pattern of lifetime income, consumption, saving, dissaving, and wealth shown in the above graph. Assume that consumption is constant over the entire lifetime, income is constant over the working lifetime, the real interest rate is zero, and there is no uncertainty about life span so that wealth equals zero at the end of life. a. If there is no populati on growth, the ratio of wealth to income will be constant for the nation. If all individuals live $T$ years and work $R$ years, the amount of wealth accumulated at the time of retirement must be enough for $T - R$ years of consumption ( $C$ per year). What is the formula for the ratio of average wealth over the whole life cycle $W$ to consumption per year, as a function of $T$ and $R$ ? That is, what is $W / C$ expressed in terms of $T$ and $R$ ?
b. If $T = 50$ and $R = 40$ , what is the numerical value of $W / C$ ?