Solved

Richie and Cathy Play a Game of Matching Fingers

Question 116

Multiple Choice

Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​
Construct the payoff matrix for the game and determine whether the game is strictly determined.
​


A) Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. R's moves Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. The game is strictly determined.
B) Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. R's moves Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. The game is not strictly determined.
C) Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. 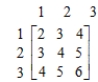Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. 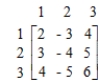R's moves Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. The game is not strictly determined.
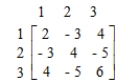D) Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. 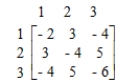Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. 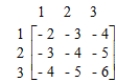R's moves Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. The game is not strictly determined.
E) Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. R's moves Richie and Cathy play a game of matching fingers. On a predetermined signal, both players simultaneously extend 1, 2, or 3 fingers from a closed fist. If the sum of the number of fingers extended is even, then Richie receives an amount in dollars equal to that sum from Cathy. If the sum of the number of fingers extended is odd, then Cathy receives an amount in dollars equal to that sum from Richie. ​ Construct the payoff matrix for the game and determine whether the game is strictly determined. ​ A) R's moves The game is strictly determined. B) R's moves The game is not strictly determined. C) R's moves The game is not strictly determined. D) R's moves The game is not strictly determined. E) R's moves The game is strictly determined. The game is strictly determined.

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q111: Find the optimal strategies, P and Q,

Q112: Is the matrix regular?<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Is

Q113: In a study of the domestic market

Q114: At the beginning of 1990, the population

Q115: Determine whether the given two-person, zero-sum matrix

Q117: Find the expected payoff E of the

Q118: Determine whether the given matrix is stochastic.

Q119: Determine whether the given matrix is stochastic.<br>​

Q120: Compute the steady-state matrix of the given

Q121: A psychologist conducts an experiment in which