Solved

Find the Expected Payoff E of the Game Whose Payoff

Question 157

Multiple Choice

Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​ Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​ ​ A) B) C) D) E) ​


A) Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​ ​ A) B) C) D) E)
B) Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​ ​ A) B) C) D) E)
C) Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​ ​ A) B) C) D) E)
D) Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​ ​ A) B) C) D) E)
E) Find the expected payoff E of the game whose payoff matrix and strategies P and Q (for the row and column players, respectively) are given. ​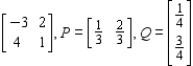 ​ A) B) 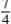C) 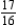D) 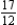E)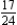

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q152: Consider the two-person, zero-sum matrix, strictly determined

Q153: Is the matrix regular?<br>​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Is

Q154: Determine whether the matrix is an absorbing

Q155: Consider the two-person, zero-sum matrix, strictly determined

Q156: Determine whether the given matrix is stochastic.

Q158: Determine whether the given two-person, zero-sum matrix

Q159: Find the steady-state vector for the transition

Q160: Determine the maximin and minimax strategies for

Q161: The transition matrix for a Markov process

Q162: Find the steady-state vector for the transition