Essay
Two dentists, Lydia Russell and Jerry Carlton, are planning to establish practices in a newly developed community. Both have allocated approximately the same total budget for advertising in the local newspaper and for the distribution of fliers announcing their practices. Because of the location of their offices, Russell is expected to get 47% of the business if both dentists advertise only in the local newspaper; if both dentists advertise through fliers, then Russell is expected to get 44% of the business; if Russell advertises exclusively in the local newspaper and Carlton advertises exclusively through fliers, then Russell is expected to get 61% of the business. Finally, if Russell advertises through fliers exclusively and Carlton advertises exclusively in the local newspaper, then Russell is expected to get 50% of the business.
Construct the payoff matrix for the game. 
 C = Carlton; R = Russell
C = Carlton; R = Russell
N = local newspaper; F = flyer 


 Is the game strictly determined?
Is the game strictly determined?
Find the optimal strategy for both Russell and Carlton.
Please round the answer to the nearest hundredth. 
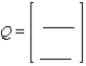
Correct Answer:

Verified
Correct Answer:
Verified
Q189: Determine whether the given matrix is stochastic.<br>
Q190: At the beginning of 1990, the population
Q191: At a certain university, three bookstores -
Q192: Find <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Find (the
Q193: Answer whether the matrix<br> <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Answer
Q195: Determine whether the matrix is regular.
Q196: Determine the maximin and minimax strategies for
Q197: The payoff matrix for a game is
Q198: Determine the maximin and minimax strategies for
Q199: Rewrite the given absorbing stochastic matrix so