Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem. A nutritionist at the Medical Center has been asked to prepare a special diet for certain patients. He has decided that the meals should contain a minimum of 400 mg of calcium, 9 mg of iron, and 35 mg of vitamin C. He has further decided that the meals are to be prepared from foods A and B. Each ounce of food A contains 35 mg of calcium, 1 mg of iron, 3 mg of vitamin C, and 3 mg of cholesterol. Each ounce of food B contains 25 mg of calcium, 0.6 mg of iron, 7 mg of vitamin C, and 7 mg of cholesterol. Find how many ounces of each type of food should be used in a meal so that the cholesterol content is minimized and the minimum requirements of calcium, iron, and vitamin C are met.
A) Minimize: 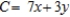 Subject to:
Subject to: 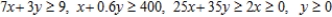
B) Minimize: 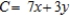 Subject to:
Subject to: 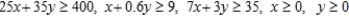
C) Minimize:  Subject to:
Subject to: 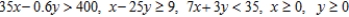
D) Minimize: 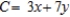 Subject to:
Subject to: 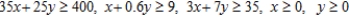
Correct Answer:

Verified
Correct Answer:
Verified
Q41: Find the graphical solution of the inequality.
Q42: Write a system of linear inequalities that
Q43: Determine graphically the solution set for the
Q44: Write a system of linear inequalities that
Q45: Determine graphically the solution set for the
Q47: Solve the linear programming problem by the
Q48: D11etermine graphically the solution set for the
Q49: Write a system of linear inequalities that
Q50: A farmer plans to plant two crops,
Q51: Solve the linear programming problem by the