Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem. A company manufactures two products, A and B, on two machines I and II. It has been determined that the company will realize a profit of $4 on each unit of product A and a profit of $3 on each unit of product B. To manufacture a unit of product A requires 5 min on machine I and 5 min on machine II. To manufacture a unit of product B requires 7 min on machine I and 4 min on machine II. There are 6 hr of machine time available on machine I and 3 hr of machine time available on machine II in each work shift. How many units of each product should be produced in each shift to maximize the company's profit?
A) Maximize: 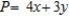 Subject to:
Subject to: 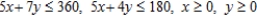
B) Maximize:  Subject to:
Subject to: 
C) Maximize: 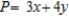 Subject to:
Subject to: 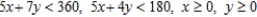
D) Maximize: 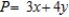 Subject to:
Subject to: 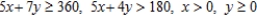
Correct Answer:

Verified
Correct Answer:
Verified
Q59: You are given a linear programming problem.
Q60: Determine graphically the solution set for the
Q61: Determine graphically the solution set for the
Q62: Bayer Pharmaceutical produces three kinds of cold
Q63: Determine graphically the solution set for the
Q65: Kane Manufacturing has a division that produces
Q66: Find the graphical solution of the inequality.
Q67: Write a system of linear inequalities that
Q68: National Business Machines manufactures two models of
Q69: Find the graphical solution of the inequality.