Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem. Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $15,000/day to operate, and it yields 30 oz of gold and 3,000 oz of silver each day. The Horseshoe Mine costs $17,000/day to operate, and it yields 65 oz of gold and 1,000 oz of silver each day. Company management has set a target of at least 550 oz of gold and 17,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost?
A) Minimize:  Subject to:
Subject to: 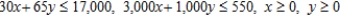
B) Minimize: 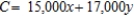 Subject to:
Subject to: 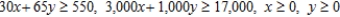
C) Minimize: 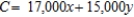 Subject to:
Subject to: 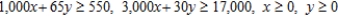
D) Minimize: 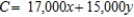 Subject to:
Subject to: 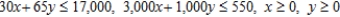
Correct Answer:

Verified
Correct Answer:
Verified
Q140: You are given a linear programming problem.Use
Q141: You are given a linear programming problem.
Q142: Write a system of linear inequalities that
Q143: Determine graphically the solution set for the
Q144: You are given a linear programming problem.
Q146: Solve the linear programming problem by the
Q147: A veterinarian has been asked to prepare
Q148: Find the graphical solution of the inequality.
Q149: Formulate but do not solve the following
Q150: Soundex produces two models of clock radios.