Multiple Choice
Formulate but do not solve the following exercise as a linear programming problem. A farmer has 140 acres of land suitable for cultivating crops A and B. The cost of cultivating crop A is $30/acre, whereas that of crop B is $80/acre. The farmer has a maximum of $5,700 available for land cultivation. Each acre of crop A requires 30 labor-hours, and each acre of crop B requires 35 labor-hours. The farmer has a maximum of 4,800 labor-hours available. If she expects to make a profit of $130/acre on crop A and $230/acre on crop B, how many acres of each crop should she plant in order to maximize her profit?
A) Maximize: 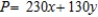 Subject to:
Subject to: 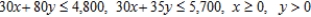
B) Maximize: 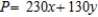 Subject to:
Subject to: 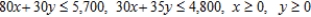
C) Maximize:  Subject to:
Subject to: 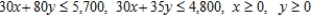
D) Maximize: 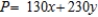 Subject to:
Subject to: 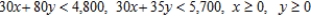
Correct Answer:

Verified
Correct Answer:
Verified
Q1: Determine graphically the solution set for the
Q2: Find the graphical solution of the inequality.
Q3: A finance company has a total of
Q4: Solve the linear programming problem by the
Q6: Formulate but do not solve the following
Q7: A company manufactures two products, A and
Q8: Write a system of linear inequalities that
Q9: Determine graphically the solution set for the
Q10: Find the graphical solution of the inequality.
Q11: Determine graphically the solution set for the