Multiple Choice
A farmer plans to plant two crops, A and B. The cost of cultivating crop A is $40/acre, whereas that of crop B is $60/acre. The farmer has a maximum of $5,400 available for land cultivation. Each acre of crop A requires 20 labor-hours, and each acre of crop B requires 25 labor-hours. The farmer has a maximum of 2,300 labor-hours available. If she expects to make a profit of $150/acre on crop A and $200/acre on crop B, how many acres of each crop should she plant in order to maximize her profit?
Find the range of values that the contribution to the profit of an acre of crop A can assume without changing the optimal solution.
Find the range of values that the resource associated with the constraint on the land available can assume.
Find the shadow price for the resource associated with the constraint on the land available.
A) Crop A = 15 acres, Crop B = 80 acres 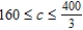
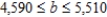
1) 25
B) Crop A = 15 acres, Crop B = 80 acres 
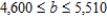
1) 25
C) Crop A = 80 acres, Crop B = 15 acres 
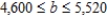
1) 25
D) Crop A = 15 acres, Crop B = 80 acres 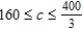
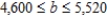
1) 25
Correct Answer:

Verified
Correct Answer:
Verified
Q86: Determine graphically the solution set for the
Q87: Write a system of linear inequalities that
Q88: Determine graphically the solution set for the
Q89: Solve the linear programming problem by the
Q90: Find the graphical solution of the inequality.
Q92: Find the optimal (maximum and/or minimum) value(s)
Q93: Write a system of linear inequalities that
Q94: Determine graphically the solution set for the
Q95: Write a system of linear inequalities that
Q96: Formulate but do not solve the following