Soundex Produces Two Models of Clock Radios

Multiple Choice

Soundex produces two models of clock radios. Model A requires 15 min of work on assembly line I and 10 min of work on assembly line II. Model B requires 12 min of work on assembly line I and 20 min of work on assembly line II. At most 21 hr of assembly time on line I and 20 hr of assembly time on line II are available each day. Soundex anticipates a profit of $12 on model A and $10 on model B. Because of previous overproduction, management decides to limit the production of model A clock radios to no more than 80/day. ​
To maximize Soundex's profit, how many clock radios of each model should be produced each day? Find the range of values that the contribution to the profit of a model A clock radio can assume without changing the optimal solution. Identify the binding and nonbinding constraints.
​

A) Produce 61 of model A, 34 of model B; maximum profit of $1,059; Range: 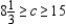; Constraints 1 and 3 are binding; constraint 2 is not.
​
B) Produce 30 of model A, 60 of model B; maximum profit of $1,020; Range: 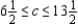; Constraints 1 and 2 are binding; constraint 3 is not.
​
C) Produce 60 of model A, 30 of model B; maximum profit of $1,020; Range: 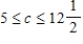; Constraints 1 and 2 are binding; constraint 3 is not.
​