Kane Manufacturing Has a Division That Produces Two Models of Fireplace

Multiple Choice

Kane Manufacturing has a division that produces two models of fireplace grates, model A and model B. To produce each model A grate requires 3 lb of cast iron and 6 min of labor. To produce each model B grate requires 4 lb of cast iron and 3 min of labor. The profit for each model A grate is $2, and the profit for each model B grate is $1.50. 1,000 lb of cast iron and 22 labor-hours are available for the production of grates each day. Because of an excess inventory of model A grates, management has decided to limit the production of model A grates to no more than 200 grates per day. How many grates of each model should the division produce daily to maximize Kane's profits? The range of values that the coefficient of x can assume without changing the optimal solution is 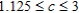If the contribution to the profit of a model A grate is changed to $1.90/grate, will the original optimal solution still hold? What will be the new optimal solution?

A) No; 136 grates of model A; 136 grates of model B; optimal profit is $486.70
B) Yes; 152 grates of model A; 152 grates of model B; optimal profit is $486.70
C) Yes; 152 grates of model A; 136 grates of model B; optimal profit is $492.80
D) No; 136 grates of model A; 152 grates of model B; optimal profit is $492.80