Ace Novelty Wishes to Produce Two Types of Souvenirs: Type

Multiple Choice

Ace Novelty wishes to produce two types of souvenirs: type A and type B. Each type-A souvenir will result in a profit of $1.00, and each type-B souvenir will result in a profit of $1.20. To manufacture a type-A souvenir requires 2 minutes on machine I and 1 minute on machine II. A type-B souvenir requires 1 minute on machine I and 3 minutes on machine II. There are 3 hours available on machine I and 5 hours available on machine II for processing the order. Let x be the number of type-A souvenirs and y be the number of type-B souvenirs to be made. Then, the problem can be reduced to a linear programming problem with the objective function 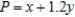and constraints 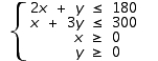What will be the optimal profit of the company if the contribution to the profit of a type-B souvenir is $2.30 (with the contribution to the profit of a type-A souvenir held at $1.00) ?

A) $241.20
B) $248.10
C) $261.90
D) $234.30
E) $255.00