Multiple Choice
Determine the value of k for which the system of linear equations has infinitely many solutions. Then find all solutions corresponding to this value of k. 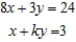
A)  . The solutions are
. The solutions are 
B) 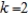 . The solutions are
. The solutions are 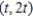
C)  . The solutions are
. The solutions are 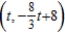
D)  . The solutions are
. The solutions are 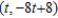
Correct Answer:

Verified
Correct Answer:
Verified
Q303: A simple economy consists of two industries:
Q304: Perform the subtraction. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Perform the
Q305: Find the transpose of the given matrix.
Q306: Determine the value of k for which
Q307: A dietitian wishes to plan a meal
Q308: Determine whether the system of linear equations
Q309: Solve the system of linear equations, using
Q310: Solve the system of linear equations, using
Q312: Perform the subtraction. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Perform the
Q313: The total number of passengers riding a