Solved

Solve the System of Linear Equations, Using the Gauss-Jordan Elimination

Question 168

Multiple Choice

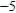
Solve the system of linear equations, using the Gauss-Jordan elimination method. Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z =


A) x = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , y = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , z = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z =
B) x = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , y = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , z = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z =
C) x = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , y = 0, z = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z =
D) x = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , y = 0, z = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z =
E) x = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z = , y = 0, z = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x = , y = , z = B) x = , y = , z = C) x = , y = 0, z = D) x = , y = 0, z = E) x = , y = 0, z =

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q163: The annual interest on Sid Carrington's three

Q164: Indicate whether the matrix is in row-reduced

Q165: Jackson Farms have allotted a certain amount

Q166: Solve the system of linear equations using

Q167: Solve for u, x, y, and z

Q169: Find the matrix A such that ​

Q170: Given that the augmented matrix in row-reduced

Q171: Solve the system of linear equations using

Q172: In this problem matrix A is an

Q173: Solve the system of linear equations using