Solved

Solve the System of Linear Equations, Using the Gauss-Jordan Elimination

Question 181

Multiple Choice

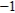Solve the system of linear equations, using the Gauss-Jordan elimination method. Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0


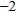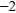A) x1 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x2 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x3 = 0
B) x1 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x2 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x3 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0
C) x1 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x2 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x3 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0
D) x1 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x2 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x3 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0
E) x1 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x2 = Solve the system of linear equations, using the Gauss-Jordan elimination method. A) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 B) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = C) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = D) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = E) x<sub>1</sub> = , x<sub>2</sub> = , x<sub>3</sub> = 0 , x3 = 0

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q176: Perform the addition. <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Perform the

Q177: <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt=" ​ A)

Q178: A simple economy consists of three sectors:

Q179: A dietitian plans a meal around three

Q180: Compute the product. ​ <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Compute

Q182: Indicate whether the matrix is in row-reduced

Q183: The total output of loudspeaker systems of

Q184: Given that the augmented matrix in rowreduced

Q185: Formulate but do not solve the problem.

Q186: Solve the matrix equation <img src="https://d2lvgg3v3hfg70.cloudfront.net/TB6027/.jpg" alt="Solve