Solved

Find the Constants M and B in the Linear Function

Question 232

Multiple Choice

Find the constants m and b in the linear function f(x) = mx + b so that f(2) = 6 and the straight line represented by f has slope - 1.


A) Find the constants m and b in the linear function f(x) = mx + b so that f(2) = 6 and the straight line represented by f has slope - 1. A) B) C) D)
B) Find the constants m and b in the linear function f(x) = mx + b so that f(2) = 6 and the straight line represented by f has slope - 1. A) B) C) D)
C) Find the constants m and b in the linear function f(x) = mx + b so that f(2) = 6 and the straight line represented by f has slope - 1. A) B) C) D)
D) Find the constants m and b in the linear function f(x) = mx + b so that f(2) = 6 and the straight line represented by f has slope - 1. A) 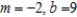B) 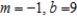C) 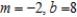D)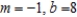

Correct Answer:

verifed

Verified

Unlock this answer now
Get Access to more Verified Answers free of charge

Related Questions

Q227: Sketch a set of coordinate axes and

Q228: The annual sales of Crimson Drug Store

Q229: Find an equation of the vertical line

Q230: Metro Department Store's annual sales (in millions

Q231: The Social Security (FICA) wage base (in

Q233: Find the equation of the least-squares line

Q234: Find the equation of the least-squares line

Q235: With computer security always a hot-button issue,

Q236: Find the distance between the given points.<br>(-

Q237: Find an equation of the circle that