Multiple Choice
Determine whether the statement is true or false. If it is true, explain why it is true. If it is false, give an example to show why it is false.
If the data consist of two distinct points, then the least-squares line is just the line that passes through the two points.
A) It is true.
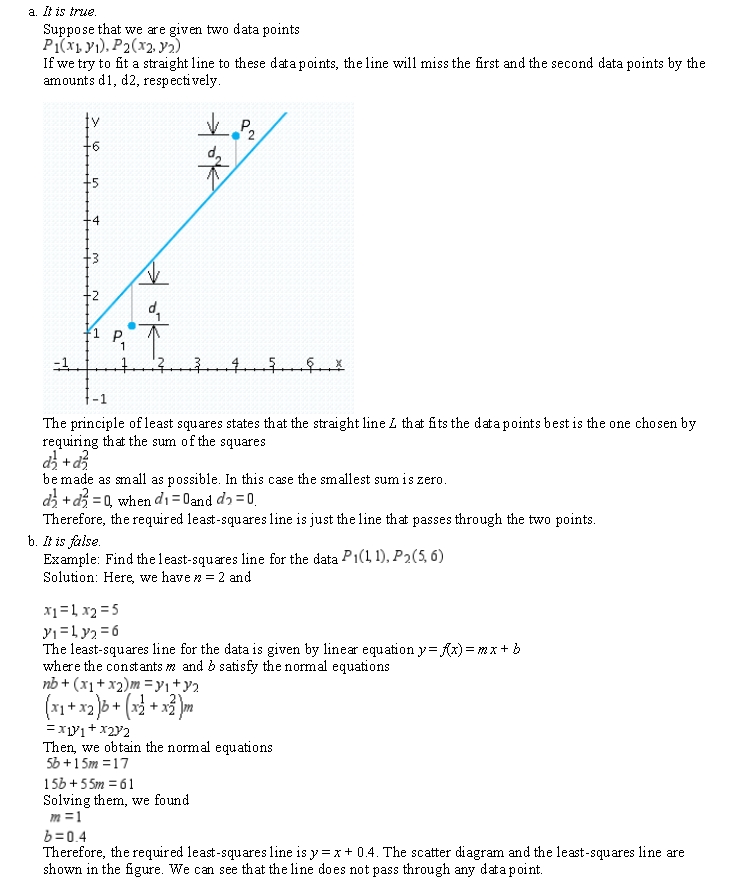
Suppose that we are given two data points 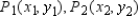
If we try to fit a straight line to these data points, the line will miss the first and the second data points by the amounts d1, d2, respectively.
The principle of least squares states that the straight line L that fits the data points best is the one chosen by requiring that the sum of the squares 
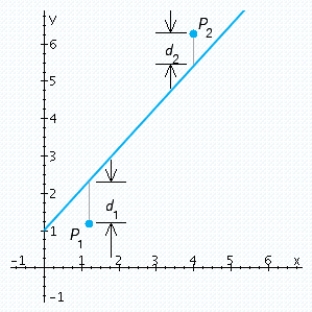
Be made as small as possible. In this case the smallest sum is zero.  , when
, when 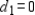 and
and 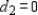 .
.
Therefore, the required least-squares line is just the line that passes through the two points.
B) It is false.
Example: Find the least-squares line for the data 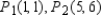 Solution: Here, we have n = 2 and
Solution: Here, we have n = 2 and 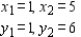
The least-squares line for the data is given by linear equation y = f(x) = mx + b
Where the constants m and b satisfy the normal equations 
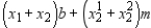
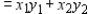 Then, we obtain the normal equations
Then, we obtain the normal equations 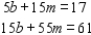 Solving them, we found
Solving them, we found 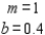 Therefore, the required least-squares line is y = x + 0.4. The scatter diagram and the least-squares line are shown in the figure. We can see that the line does not pass through any data point.
Therefore, the required least-squares line is y = x + 0.4. The scatter diagram and the least-squares line are shown in the figure. We can see that the line does not pass through any data point. 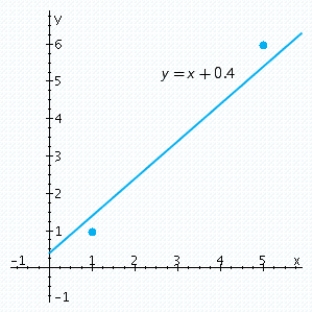
Correct Answer:

Verified
Correct Answer:
Verified
Q17: Find an equation of the circle that
Q18: Match the statement with one of the
Q19: Find the point of intersection of the
Q20: Determine whether the statement is true or
Q21: Determine whether the lines through the given
Q23: Determine whether the statement is true or
Q24: Assume that a certain commodity's demand equation
Q25: Find an equation of the line that
Q26: The demand equation for the Schmidt-3000 fax
Q27: Sketch a set of coordinate axes and