Deck 14: Simple Linear Regression Analysis
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/147
Play
Full screen (f)
Deck 14: Simple Linear Regression Analysis
1
The correlation coefficient is the ratio of explained variation to total variation.
False
2
In simple linear regression analysis, we assume that the variance of the independent variable (X) is equal to the variance of the dependent variable (Y).
False
3
The error term is the difference between an individual value of the dependent variable and the corresponding mean value of the dependent variable.
False
4
The experimental region is the range of the previously observed values of the dependent variable.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
5
The dependent variable is the variable that is being described or predicted.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
6
In simple regression analysis, r2 is a percentage measure and measures the proportion of the variation explained by the simple linear regression model.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
7
In a simple linear regression model, the coefficient of determination not only indicates the strength of the relationship between the independent and dependent variables, but also shows whether the relationship is positive or negative.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
8
In simple linear regression analysis, if the error terms exhibit a positive or negative autocorrelation over time, then the assumption of constant variance is violated.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
9
The standard error of the estimate (standard error) is the estimated standard deviation of the distribution of the independent variable (X) for all values of the dependent variable (Y).

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
10
A simple linear regression model is an equation that describes the straight-line relationship between a dependent variable and an independent variable.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
11
A significant positive correlation between X and Y implies that changes in X cause Y to change.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
12
The simple coefficient of determination is the proportion of total variation explained by the regression line.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
13
The slope of the simple linear regression equation represents the average change in the value of the dependent variable per unit change in the independent variable (X).

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
14
The least squares simple linear regression line minimizes the sum of the vertical deviations between the line and the data points.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
15
The notation Ŷ refers to the average value of the dependent variable Y.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
16
If r = −1, then we can conclude that there is a perfect relationship between X and Y.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
17
When using simple regression analysis, if there is a strong correlation between the independent and dependent variables, then we can conclude that an increase in the value of the independent variable causes an increase in the value of the dependent variable.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
18
The residual is the difference between the observed value of the dependent variable and the predicted value of the dependent variable.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
19
When there is positive autocorrelation, over time, negative error terms are followed by positive error terms and positive error terms are followed by negative error terms.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
20
The estimated simple linear regression equation minimizes the sum of the squared deviations between each value of Y and the line.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
21
The point estimate of the variance in a regression model is
A) SSE.
B) b0.
C) MSE.
D) b1.
A) SSE.
B) b0.
C) MSE.
D) b1.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
22
If successive values of the residuals are close together, then there is a ________ autocorrelation and the value of the Durbin-Watson statistic is ________.
A) negative; large
B) positive; small
C) negative; small
D) positive; large
A) negative; large
B) positive; small
C) negative; small
D) positive; large

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
23
When using simple linear regression, we would like to use confidence intervals for the ________ and prediction intervals for the ________ at a given value of x.
A) Individual y-value; mean y-value
B) mean y-value; individual y-value
C) slope; mean slope
D) y-intercept; mean y-intercept
A) Individual y-value; mean y-value
B) mean y-value; individual y-value
C) slope; mean slope
D) y-intercept; mean y-intercept

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
24
In a simple linear regression analysis, the correlation coefficient (a) and the slope (b) ________ have the same sign.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
25
The correlation coefficient may assume any value between
A) 0 and 1.
B) −∞ and ∞.
C) 0 and 8.
D) −1 and 1.
E) −1 and 0.
A) 0 and 1.
B) −∞ and ∞.
C) 0 and 8.
D) −1 and 1.
E) −1 and 0.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
26
In simple regression analysis, the standard error is ________ greater than the standard deviation of y values.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
27
If the Durbin-Watson statistic is greater than (4 − dL), then we conclude that
A) there is significant positive autocorrelation.
B) there is significant negative autocorrelation.
C) there is significant autocorrelation, but we cannot identify whether it is positive or negative.
D) the test result is inconclusive.
A) there is significant positive autocorrelation.
B) there is significant negative autocorrelation.
C) there is significant autocorrelation, but we cannot identify whether it is positive or negative.
D) the test result is inconclusive.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
28
A simple regression analysis with 20 observations would yield ________ degrees of freedom error and ________degrees of freedom total.
A) 1; 20
B) 18; 19
C) 19; 20
D) 1; 19
E) 18; 20
A) 1; 20
B) 18; 19
C) 19; 20
D) 1; 19
E) 18; 20

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
29
For the same value of X (independent variable), the confidence interval for the average value of Y (dependent variable) is ________ the prediction interval for the individual value of Y.
A) larger than
B) smaller than
C) the same as
D) sometimes larger than, sometimes smaller than
A) larger than
B) smaller than
C) the same as
D) sometimes larger than, sometimes smaller than

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
30
The least squares regression line minimizes the sum of the
A) differences between actual and predicted Y values.
B) absolute deviations between actual and predicted Y values.
C) absolute deviations between actual and predicted X values.
D) squared differences between actual and predicted Y values.
E) squared differences between actual and predicted X values.
A) differences between actual and predicted Y values.
B) absolute deviations between actual and predicted Y values.
C) absolute deviations between actual and predicted X values.
D) squared differences between actual and predicted Y values.
E) squared differences between actual and predicted X values.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
31
What value of the Durbin-Watson statistic indicates that there is no autocorrelation present in time-ordered data?
A) 1
B) −1
C) 2
D) −2
E) 0
A) 1
B) −1
C) 2
D) −2
E) 0

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
32
In simple regression analysis, the quantity Σ(Ŷ − Ȳ)2 is called the ________ sum of squares.
A) total
B) explained
C) unexplained
D) error
A) total
B) explained
C) unexplained
D) error

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
33
All of the following are assumptions of the error terms in the simple linear regression model except
A) errors are normally distributed.
B) error terms have a mean of zero.
C) error terms have a constant variance.
D) error terms are dependent on each other.
A) errors are normally distributed.
B) error terms have a mean of zero.
C) error terms have a constant variance.
D) error terms are dependent on each other.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
34
The Durbin-Watson test statistic ranges from
A) −4 to 4.
B) 0 to 4.
C) 0 to 3.
D) −1 to 1.
E) 0 to 1.
A) −4 to 4.
B) 0 to 4.
C) 0 to 3.
D) −1 to 1.
E) 0 to 1.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
35
The ________ measures the strength of the linear relationship between the dependent variable and the independent variable.
A) correlation coefficient
B) distance value
C) Y-intercept
D) residual
A) correlation coefficient
B) distance value
C) Y-intercept
D) residual

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
36
The ________ the r2 and the ________ the s (standard error), the stronger the relationship between the dependent variable and the independent variable.
A) higher; lower
B) lower; higher
C) lower; lower
D) higher; higher
A) higher; lower
B) lower; higher
C) lower; lower
D) higher; higher

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
37
If the Durbin-Watson statistic is less than dL, then we conclude that
A) there is significant positive autocorrelation.
B) there is significant negative autocorrelation.
C) there is significant autocorrelation, but we cannot identify whether it is positive or negative.
D) the test results are inconclusive.
A) there is significant positive autocorrelation.
B) there is significant negative autocorrelation.
C) there is significant autocorrelation, but we cannot identify whether it is positive or negative.
D) the test results are inconclusive.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
38
Which of the following is a violation of one of the major assumptions of the simple regression model?
A) The error terms are independent of each other.
B) A histogram of the residuals forms a bell-shaped, symmetrical curve.
C) The error terms show no pattern.
D) As the value of x increases, the value of the error term also increases.
A) The error terms are independent of each other.
B) A histogram of the residuals forms a bell-shaped, symmetrical curve.
C) The error terms show no pattern.
D) As the value of x increases, the value of the error term also increases.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
39
In simple regression analysis, the quantity that gives the amount by which Y (dependent variable) changes for a unit change in X (independent variable) is called the
A) coefficient of determination.
B) slope of the regression line.
C) y-intercept of the regression line.
D) correlation coefficient.
E) standard error.
A) coefficient of determination.
B) slope of the regression line.
C) y-intercept of the regression line.
D) correlation coefficient.
E) standard error.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
40
When the assumption of ________ residuals (error terms) is violated, the Durbin-Watson statistic is used to test to determine if there is significant ________ among the residuals.
A) normality; probability
B) independent; probability
C) independent; autocorrelation
D) normality; autocorrelation
A) normality; probability
B) independent; probability
C) independent; autocorrelation
D) normality; autocorrelation

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
41
In a simple regression analysis for a given data set, if the null hypothesis β = 0 is rejected, then the null hypothesis ρ = 0 is also rejected. This statement is ________ true.
A) always
B) never
C) sometimes
A) always
B) never
C) sometimes

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
42
The least squares point estimates of the simple linear regression model minimize the ________.
A) SS error
B) total variance
C) MS error
D) explained variance
A) SS error
B) total variance
C) MS error
D) explained variance

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
43
Which of the following is a violation of the independence assumption?
A) negative autocorrelation
B) a pattern of cyclical error terms over time
C) positive autocorrelation
D) a pattern of alternating error terms over time
E) All of the other choices are correct.
A) negative autocorrelation
B) a pattern of cyclical error terms over time
C) positive autocorrelation
D) a pattern of alternating error terms over time
E) All of the other choices are correct.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
44
The ________ is the range of the previously observed values of x.
A) population region
B) experimental region
C) slope
D) coefficient of determination
A) population region
B) experimental region
C) slope
D) coefficient of determination

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
45
The ________ assumption requires that all variation around the regression line should be equal at all possible values (levels) of the ________variable.
A) control variance; independent
B) control variance; dependent
C) constant variance; independent
D) constant variance; dependent
A) control variance; independent
B) control variance; dependent
C) constant variance; independent
D) constant variance; dependent

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
46
When the constant variance assumption holds, a plot of the residual versus x
A) fans out.
B) funnels in.
C) fans out, but then funnels in.
D) forms a horizontal band pattern.
E) suggests an increasing error variance.
A) fans out.
B) funnels in.
C) fans out, but then funnels in.
D) forms a horizontal band pattern.
E) suggests an increasing error variance.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
47
The range for r2 is between 0 and 1, and the range for r is between ________.
A) 0 and 1
B) −1 and 1
C) −1 and 0
D) There is no limit for r.
A) 0 and 1
B) −1 and 1
C) −1 and 0
D) There is no limit for r.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
48
Any value of the error term in a regression model ________ any other value of the error term.
A) increases with
B) is dependent on
C) is independent of
D) is exactly the same as
A) increases with
B) is dependent on
C) is independent of
D) is exactly the same as

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
49
The strength of the relationship between two quantitative variables can be measured by
A) the slope of a simple linear regression equation.
B) the y-intercept of the simple linear regression equation.
C) the coefficient of correlation.
D) the coefficient of determination.
E) both the coefficient of correlation and the coefficient of determination.
A) the slope of a simple linear regression equation.
B) the y-intercept of the simple linear regression equation.
C) the coefficient of correlation.
D) the coefficient of determination.
E) both the coefficient of correlation and the coefficient of determination.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
50
In a simple linear regression model, the slope term is the change in the mean value of y associated with ________ in x.
A) a corresponding increase
B) a variable change
C) no change
D) a one-unit increase
A) a corresponding increase
B) a variable change
C) no change
D) a one-unit increase

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
51
In simple regression analysis, if the correlation coefficient is a positive value, then
A) the y-intercept must also be a positive value.
B) the coefficient of determination can be either positive or negative, depending on the value of the slope.
C) the least squares regression equation could have either a positive or a negative slope.
D) the slope of the regression line must also be positive.
E) the standard error of estimate can have either a positive or a negative value.
A) the y-intercept must also be a positive value.
B) the coefficient of determination can be either positive or negative, depending on the value of the slope.
C) the least squares regression equation could have either a positive or a negative slope.
D) the slope of the regression line must also be positive.
E) the standard error of estimate can have either a positive or a negative value.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
52
For a given data set, value of X, and confidence level, if all the other factors are constant, the confidence interval for the mean value of Y will ________ be wider than the corresponding prediction interval for the individual value of Y.
A) always
B) sometimes
C) never
A) always
B) sometimes
C) never

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
53
The following results were obtained as part of a simple regression analysis. r2 = .9162
F statistic from the F table = 3.59
Calculated value of F from the ANOVA table = 81.87
Α = .05
P-value = .000
The null hypothesis of no linear relationship between the dependent variable and the independent variable
A) is rejected.
B) cannot be tested with the given information.
C) is not rejected.
D) is not an appropriate null hypothesis for this situation.
F statistic from the F table = 3.59
Calculated value of F from the ANOVA table = 81.87
Α = .05
P-value = .000
The null hypothesis of no linear relationship between the dependent variable and the independent variable
A) is rejected.
B) cannot be tested with the given information.
C) is not rejected.
D) is not an appropriate null hypothesis for this situation.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
54
The ________ of the simple linear regression model is the value of y when the mean value of x is zero.
A) y-intercept
B) slope
C) independent variable
D) response variable
A) y-intercept
B) slope
C) independent variable
D) response variable

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
55
The simple linear regression (least squares method) minimizes
A) the explained variation.
B) SSyy.
C) total variation.
D) SSxx.
E) SSE.
A) the explained variation.
B) SSyy.
C) total variation.
D) SSxx.
E) SSE.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
56
If there is significant autocorrelation present in a data set, the ________ assumption is violated.
A) normality
B) independence of error terms
C) μ = 0
D) constant variation
A) normality
B) independence of error terms
C) μ = 0
D) constant variation

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
57
After plotting the data points on a scatter diagram, we have observed an inverse relationship between the independent variable (X) and the dependent variable (Y). Therefore, we can expect both the sample ________ and the sample ________ to be negative values.
A) intercept, slope
B) slope; coefficient of determination
C) intercept; correlation coefficient
D) slope; correlation coefficient
E) slope; standard error of estimate
A) intercept, slope
B) slope; coefficient of determination
C) intercept; correlation coefficient
D) slope; correlation coefficient
E) slope; standard error of estimate

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
58
In a simple linear regression model, the intercept term is the mean value of y when x equals ________.
A) 1
B) 0
C) −1
D) y
A) 1
B) 0
C) −1
D) y

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
59
For the same set of observations on a specified dependent variable, two different independent variables were used to develop two separate simple linear regression models. A portion of the results is presented below. 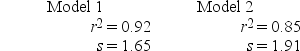 Based on the results given above, we can conclude that
Based on the results given above, we can conclude that
A) a prediction based on Model 1 is better than a prediction based on Model 2.
B) a prediction based on Model 2 is better than a prediction based on Model 1.
C) there is no difference in the predictive ability between Model 1 and Model 2.
D) there is not sufficient information to determine which of the two models is superior for prediction purposes.
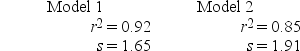 Based on the results given above, we can conclude that
Based on the results given above, we can conclude thatA) a prediction based on Model 1 is better than a prediction based on Model 2.
B) a prediction based on Model 2 is better than a prediction based on Model 1.
C) there is no difference in the predictive ability between Model 1 and Model 2.
D) there is not sufficient information to determine which of the two models is superior for prediction purposes.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
60
The coefficient of determination measures the ________ explained by the simple linear regression model.
A) correlation
B) proportion of variation
C) standard error
D) mean square error
A) correlation
B) proportion of variation
C) standard error
D) mean square error

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
61
The ________ is the proportion of the total variation in the dependent variable explained by the regression model.
A) coefficient of determination
B) correlation coefficient
C) slope
D) standard error
A) coefficient of determination
B) correlation coefficient
C) slope
D) standard error

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
62
Regression Analysis
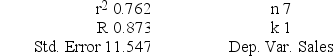 ANOVA
ANOVA
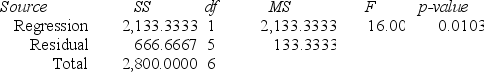 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
What is the value of the simple coefficient of determination?
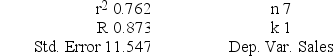 ANOVA
ANOVA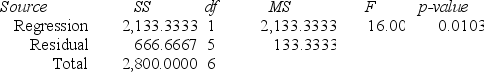 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.What is the value of the simple coefficient of determination?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
63
A ________ measures the strength of the relationship between a dependent variable (Y) and an independent variable (X).
A) coefficient of determination
B) correlation coefficient
C) slope
D) standard error
A) coefficient of determination
B) correlation coefficient
C) slope
D) standard error

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
64
Regression Analysis
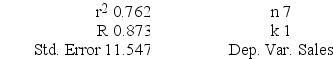 ANOVA
ANOVA
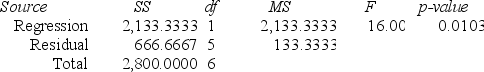 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
What are the limits of the 95 percent confidence interval for the population slope?
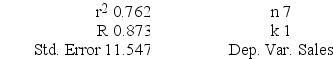 ANOVA
ANOVA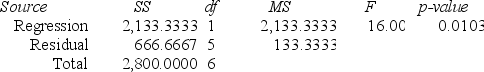 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.What are the limits of the 95 percent confidence interval for the population slope?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
65
The following results were obtained from a simple regression analysis.
Ŷ = 37.2895 − (1.2024)X
r2 = .6744sb = .2934
What is the proportion of the variation explained by the simple linear regression model?
Ŷ = 37.2895 − (1.2024)X
r2 = .6744sb = .2934
What is the proportion of the variation explained by the simple linear regression model?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
66
Use the following results obtained from a simple linear regression analysis with 12 observations. 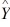 = 37.2895 − (1.2024)X
= 37.2895 − (1.2024)X
r2 = .6744sb = .2934
Test to determine if there is a significant negative relationship between the independent and dependent variables at α = .05. Give the test statistic and the resulting conclusion.
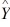 = 37.2895 − (1.2024)X
= 37.2895 − (1.2024)Xr2 = .6744sb = .2934
Test to determine if there is a significant negative relationship between the independent and dependent variables at α = .05. Give the test statistic and the resulting conclusion.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
67
An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Using the simple linear regression model, find the estimated y-intercept and slope and write the equation of the least squares regression line.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Using the simple linear regression model, find the estimated y-intercept and slope and write the equation of the least squares regression line.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
68
An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below. Use the simple linear regression model.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Determine SSE and SS(Total).
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Determine SSE and SS(Total).

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
69
Regression Analysis.
 ANOVA
ANOVA
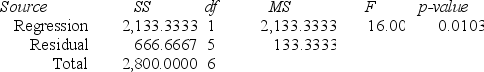 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
Determine a 95 percent confidence interval estimate of the daily average store sales based on $3,000 advertising expenditures. The distance value for this particular prediction is reported as .164.
 ANOVA
ANOVA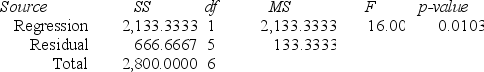 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.Determine a 95 percent confidence interval estimate of the daily average store sales based on $3,000 advertising expenditures. The distance value for this particular prediction is reported as .164.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
70
Regression Analysis
 ANOVA
ANOVA
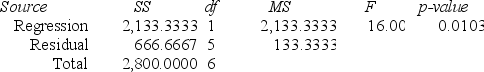 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
At a significance level of .05, test the significance of the slope and state your conclusion.
 ANOVA
ANOVA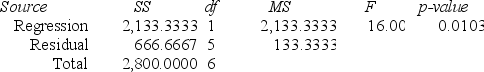 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.At a significance level of .05, test the significance of the slope and state your conclusion.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
71
Regression Analysis
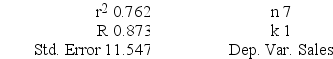 ANOVA
ANOVA
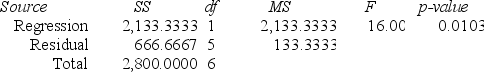 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
What is the estimated simple linear regression equation?
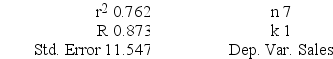 ANOVA
ANOVA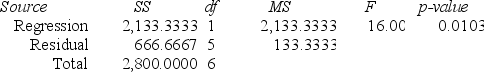 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.What is the estimated simple linear regression equation?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
72
The following results were obtained from a simple regression analysis.
Ŷ = 37.2895 − 1.2024X
r2 = .6744sb = .2934
When X (independent variable) is equal to zero, what is the estimated value of Y (dependent variable)?
Ŷ = 37.2895 − 1.2024X
r2 = .6744sb = .2934
When X (independent variable) is equal to zero, what is the estimated value of Y (dependent variable)?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
73
If one of the assumptions of the regression model is violated, performing data transformations on the ________ can remedy the situation.
A) independent variable
B) slope
C) predictor variable
D) response variable
A) independent variable
B) slope
C) predictor variable
D) response variable

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
74
The following results were obtained from a simple regression analysis.
Ŷ = 37.2895 − 1.2024X
r2 = .6744 sb = .2934
For each unit change in X (independent variable), what is the estimated change in Y (dependent variable)?
Ŷ = 37.2895 − 1.2024X
r2 = .6744 sb = .2934
For each unit change in X (independent variable), what is the estimated change in Y (dependent variable)?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
75
An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below. Use the simple linear regression model.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Determine the standard error.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Determine the standard error.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
76
The ________ distribution is used for testing the significance of the slope term.
A) t
B) z
C) r
D) r2
A) t
B) z
C) r
D) r2

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
77
An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Using the simple linear regression model, find the estimated y-intercept.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Using the simple linear regression model, find the estimated y-intercept.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
78
Regression Analysis.
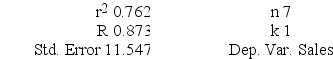 ANOVA
ANOVA
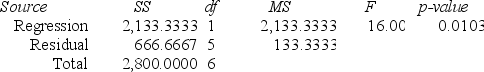 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
What are the limits of the 99 percent prediction interval of the daily sales in dollars of an individual grocery store that has spent $3,000 on advertising expenditures? The distance value for this particular prediction is reported as .164.
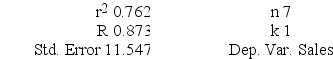 ANOVA
ANOVA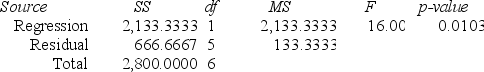 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.What are the limits of the 99 percent prediction interval of the daily sales in dollars of an individual grocery store that has spent $3,000 on advertising expenditures? The distance value for this particular prediction is reported as .164.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
79
An experiment was performed on a certain metal to determine if the strength is a function of heating time. Results based on 10 metal sheets are given below. Use the simple linear regression model.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Determine the value of the F statistic.
∑X = 30
∑X2 = 104
∑Y = 40
∑Y2 = 178
∑XY = 134
Determine the value of the F statistic.

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck
80
Regression Analysis
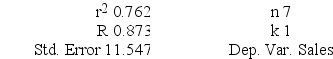 ANOVA
ANOVA
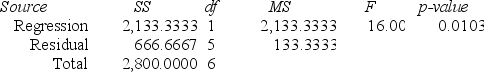 Regression output
Regression output
 A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
If the manager decides to spend $3,000 on advertising, based on the simple linear regression results given above, what are the estimated sales?
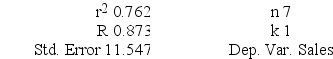 ANOVA
ANOVA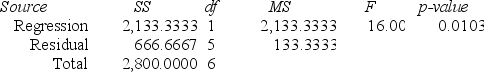 Regression output
Regression output A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.
A local grocery store wants to predict its daily sales in dollars. The manager believes that the amount of newspaper advertising significantly affects sales. He randomly selects 7 days of data consisting of daily grocery store sales (in thousands of dollars) and advertising expenditures (in thousands of dollars). The Excel/MegaStat output given above summarizes the results of the regression model.If the manager decides to spend $3,000 on advertising, based on the simple linear regression results given above, what are the estimated sales?

Unlock Deck
Unlock for access to all 147 flashcards in this deck.
Unlock Deck
k this deck


