Deck 12: Markov Process Models
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/49
Play
Full screen (f)
Deck 12: Markov Process Models
1
Which of the following is a necessary characteristic of a Markovian transition matrix?
A)Periodicity.
B)Column numbers sum to 1.
C)Square (number of rows = number of columns).
D)Singularity.
A)Periodicity.
B)Column numbers sum to 1.
C)Square (number of rows = number of columns).
D)Singularity.
C
2
All of the following are necessary characteristics of a Markov process except:
A)a countable number of stages.
B)a countable number of states per stage.
C)at least one absorbing state.
D)the memoryless property.
A)a countable number of stages.
B)a countable number of states per stage.
C)at least one absorbing state.
D)the memoryless property.
C
3
Although the number of possible states in a Markov process may be infinite, they must be countably infinite.
True
4
Every Markov process has at least one absorbing state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
5
Markov processes are a powerful decision making tool useful in explaining the behavior of systems and determining limiting behavior.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
6
"How you arrived at where you are now has no bearing on where you go next." This, simply put, is the Markovian memoryless property.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
7
A stage in a Markov process always corresponds to a fixed time period.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
8
The values towards which state probabilities converge are the steady-state probabilities.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
9
Consider the transition matrix:
The steady-state probability of being in state 1 is approximately:
A).177
B).231
C).300
D).403
The steady-state probability of being in state 1 is approximately:
A).177
B).231
C).300
D).403

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
10
All Markov processes eventually converge to a steady-state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
11
All Markov processes exhibit some form of periodicity.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
12
The transition matrix 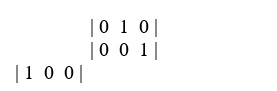
Represents what type of Markov process?
A)Periodic.
B)Absorbing.
C)Independent.
D)Nonrecurrent.
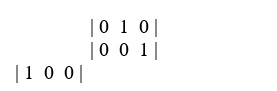
Represents what type of Markov process?
A)Periodic.
B)Absorbing.
C)Independent.
D)Nonrecurrent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
13
In a Markovian transition matrix, each column's probabilities sum to 1.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
14
For Markov processes with absorbing states, steady-state behavior is independent of the initial process state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
15
Once a process reaches steady-state, the state probabilities will never change.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
16
In a Markov process, an absorbing state is a special type of transient state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
17
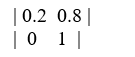 This transition matrix represents what type of Markov process?
This transition matrix represents what type of Markov process?A)Periodic.
B)Absorbing.
C)Independent.
D)Nonrecurrent.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
18
State probabilities for any given stage must sum to 1.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
19
Markovian transition matrices are necessarily square.That is, there are exactly the same number of rows as there are columns.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
20
If all the rows of a transition matrix are identical, there will be no transient states.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
21
What is the fundamental matrix for a Markov process with absorbing states?
A)A matrix composed of the identity submatrix, a zero submatrix, a submatrix of the transition probabilities between the non-absorbing states and the absorbing states, and a submatrix of transition probabilities between the non-absorbing states.
B)A matrix representing the average number of times the process visits the non-absorbing states.
C)The inverse of the identity matrix minus the matrix of the transition probabilities between the non-absorbing states and the absorbing states.
D)The matrix product of the limiting transition matrix and the matrix of transition probabilities between the non-absorbing states.
A)A matrix composed of the identity submatrix, a zero submatrix, a submatrix of the transition probabilities between the non-absorbing states and the absorbing states, and a submatrix of transition probabilities between the non-absorbing states.
B)A matrix representing the average number of times the process visits the non-absorbing states.
C)The inverse of the identity matrix minus the matrix of the transition probabilities between the non-absorbing states and the absorbing states.
D)The matrix product of the limiting transition matrix and the matrix of transition probabilities between the non-absorbing states.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
22
If we perform the calculations for steady-state probabilities for a Markov process with periodic behavior, what do we get?
A)Steady-state probabilities.
B)An unsolvable set of equations.
C)The fundamental matrix.
D)The long run percentage of time the process will be in each state.
A)Steady-state probabilities.
B)An unsolvable set of equations.
C)The fundamental matrix.
D)The long run percentage of time the process will be in each state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
23
If a Markov process consists of two absorbing states and two nonabsorbing states, the limiting probabilities for the nonabsorbing states will:
A)both equal zero.
B)be 0.5 and 0.5.
C)be identical to the transient state probabilities.
D)depend on the state vector.
A)both equal zero.
B)be 0.5 and 0.5.
C)be identical to the transient state probabilities.
D)depend on the state vector.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
24
If we add up the values in the n rows of the fundamental matrix for a Markov process with absorbing states, what is the result?
A)The rows each add to 1.
B)The limiting probability for each state.
C)A meaningless number.
D)The mean time until absorption for each state.
A)The rows each add to 1.
B)The limiting probability for each state.
C)A meaningless number.
D)The mean time until absorption for each state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
25
The Department of Motor Vehicles (DMV) has 4 stations for driver's license renewal:- fee payment
- eyesight test
- driving record check
- picture taking.
An applicant may start at any station and go from any station to any other station.Generally, an applicant will go to the unvisited station with the shortest line.If we model the stations as "states," can we use a Markov chain to model the DMV renewal process?
- eyesight test
- driving record check
- picture taking.
An applicant may start at any station and go from any station to any other station.Generally, an applicant will go to the unvisited station with the shortest line.If we model the stations as "states," can we use a Markov chain to model the DMV renewal process?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
26
Retired people often return to the workforce.If a retired woman returns to work at the same place from which she retired -- even if only part time or for a limited term -- that signifies that retirement is not a:
A)transient state.
B)steady-state.
C)periodic state.
D)absorbing state.
A)transient state.
B)steady-state.
C)periodic state.
D)absorbing state.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
27
A firm displeased with its projected steady-state market share may try to improve the situation by taking steps which hopefully will:
A)extend the number of stages.
B)alter the transition matrix.
C)better its transient state standing.
D)reduce the number of recurrent states.
A)extend the number of stages.
B)alter the transition matrix.
C)better its transient state standing.
D)reduce the number of recurrent states.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
28
A state vector is used for determining the:
A)number of stages until steady-state is reached.
B)probability that the process is in a given state.
C)existence of absorbing states.
D)values of transient state probabilities.
A)number of stages until steady-state is reached.
B)probability that the process is in a given state.
C)existence of absorbing states.
D)values of transient state probabilities.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
29
The "mean recurrence time" for a state in a Markov process:
A)is the average time it takes to return to that given state.
B)is the complement of the steady-state value.
C)only applies to processes with absorbing states.
D)depends upon the total number of stages involved.
A)is the average time it takes to return to that given state.
B)is the complement of the steady-state value.
C)only applies to processes with absorbing states.
D)depends upon the total number of stages involved.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
30
What is the steady-state significance, if any, of a zero in the transition matrix?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
31
In determining steady-state behavior for a process with absorbing states, the subdivision of the transition matrix yields:
A)an identity submatrix, but no zero submatrix.
B)no identity submatrix, but a zero submatrix.
C)both an identity submatrix and a zero submatrix.
D)neither an identity submatrix nor a zero submatrix.
A)an identity submatrix, but no zero submatrix.
B)no identity submatrix, but a zero submatrix.
C)both an identity submatrix and a zero submatrix.
D)neither an identity submatrix nor a zero submatrix.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
32
A gambler has an opportunity to play a coin tossing game in which he wins his wager with probability .49 and loses his wager with probability .51.Suppose the gambler's initial stake is $40 and the gambler will continue to make $10 bets until his fortune either reaches $0 or $100 (at which time play will stop).Which of the following statements is true?
A)Increasing the amount of each wager from $10 to $20 will increase the expected playing time.
B)Increasing the initial stake to $50 will increase the expected playing time.
C)Reducing the initial stake to $20 will increase the expected playing time.
D)Increasing the probability of winning from .49 to 1.0 will increase the expected playing time.
A)Increasing the amount of each wager from $10 to $20 will increase the expected playing time.
B)Increasing the initial stake to $50 will increase the expected playing time.
C)Reducing the initial stake to $20 will increase the expected playing time.
D)Increasing the probability of winning from .49 to 1.0 will increase the expected playing time.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
33
For a Markov process with absorbing states, we define Π(j) = state vector at stage j N = fundamental matrix
I = identity matrix
Q = matrix of transition probabilities between non-absorbing states
R = matrix of transition probabilities between non-absorbing states and absorbing states
The limiting state probabilities equal:
A)Π(1) * N * R
B)I * R * Q
C)(I - Q)-1
D)Π(1) * N * Q
I = identity matrix
Q = matrix of transition probabilities between non-absorbing states
R = matrix of transition probabilities between non-absorbing states and absorbing states
The limiting state probabilities equal:
A)Π(1) * N * R
B)I * R * Q
C)(I - Q)-1
D)Π(1) * N * Q

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
34
Charles dines out twice a week.On Tuesdays, he always frequents the same Mexican restaurant; on Thursdays, he randomizes between Greek, Italian, or Thai (but never Mexican).Is this transient, periodic, or recurrent behavior?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
35
In a Markovian system, is it possible to have only one absorbing state?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
36
Steady-state probabilities are independent of the initial state if:
A)the number of initial states is finite.
B)there are no absorbing states.
C)the number of states and stages are equal.
D)the process generates a fixed number of transient states.
A)the number of initial states is finite.
B)there are no absorbing states.
C)the number of states and stages are equal.
D)the process generates a fixed number of transient states.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
37
In a Markov process, what determines the duration of a stage?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
38
The state vector for stage j of a Markov chain with n states:
A)is a 1 x n matrix.
B)contains transition probabilities for stage j.
C)contains only nonzero values.
D)contains the steady-state probabilities.
A)is a 1 x n matrix.
B)contains transition probabilities for stage j.
C)contains only nonzero values.
D)contains the steady-state probabilities.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
39
A Markovian system is currently at stage 1.To determine the state of the system at stage 6, we must have, in addition to the transition matrix, the state probabilities at:
A)stage 5.
B)stage 1.
C)any stage, up to and including 5.
D)no stage values are needed.
A)stage 5.
B)stage 1.
C)any stage, up to and including 5.
D)no stage values are needed.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
40
Regarding a transition matrix which possesses an absorbing state:
A)All row values will not sum to 1.
B)There will be a complementary absorbing state.
C)At least two columns will be identical.
D)That state's row will consist of a "1" and "0's".
A)All row values will not sum to 1.
B)There will be a complementary absorbing state.
C)At least two columns will be identical.
D)That state's row will consist of a "1" and "0's".

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
41
When calculating steady-state probabilities, we multiply the vector of n unknown values times the transition probability matrix to produce n equations with n unknowns.Why do we arbitrarily drop one of these equations?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
42
Is this an acceptable transition matrix? Explain your answer.
| .3 .3 .4 0 |
| .2 .5 0 .3 |
| .1 .6 .2 .1 |
| .3 .3 .4 0 |
| .2 .5 0 .3 |
| .1 .6 .2 .1 |

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
43
A simple computer game using a Markov chain starts at the Cave or the Castle with equal probability and ends with Death (you lose) or Treasure (you win).The outcome depends entirely on luck.The transition probabilities are:
A.What is the average number of times you would expect to visit the Cave and the Castle, depending on which state is the starting state?
B.What is the mean time until absorption for the Cave and the Castle?
C.What is the likelihood of winning the game?
A.What is the average number of times you would expect to visit the Cave and the Castle, depending on which state is the starting state?
B.What is the mean time until absorption for the Cave and the Castle?
C.What is the likelihood of winning the game?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
44
The transition matrix for customer purchases of alkaline batteries is believed to be as follows:
A.Based on this transition matrix, what is Duracell's market share for the alkaline battery market?
B.Each 1% of the market share of the alkaline battery market is worth $3.2 million in profit.Suppose that Duracell is contemplating an advertising campaign which it believes will result in the transition probabilities for battery purchases to be as follows:
What is the most that Duracell should be willing to pay for this
campaign?
A.Based on this transition matrix, what is Duracell's market share for the alkaline battery market?
B.Each 1% of the market share of the alkaline battery market is worth $3.2 million in profit.Suppose that Duracell is contemplating an advertising campaign which it believes will result in the transition probabilities for battery purchases to be as follows:
What is the most that Duracell should be willing to pay for this
campaign?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
45
What is the minimum percentage of transition probabilities that must be nonzero?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
46
Suppose you play a coin flipping game with a friend in which a fair coin is used.If the coin comes up heads you win $1 from yourfriend, if the coin comes up tails, your friend wins $1 from you.
You have $3 and your friend has $4.You will stop the game when one
of you is broke.Determine the probability that you will win all of your friend's money.
You have $3 and your friend has $4.You will stop the game when one
of you is broke.Determine the probability that you will win all of your friend's money.

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
47
Every week a charter plane brings a group of high-stakes gamblers into Las Begas.Half the group stays and begins gambling at Hot Slots near the Strip, and the other half is housed and begins gambling at Better Bandits, some distance away.(Both hotel/casinos are owned by the same corporation.)Once an hour, dedicated shuttle buses will transport to the other
casino any of the group members who wish to try their luck at the other casino.The transition probabilities are as follows:
A.After three hours, what proportion of these gamblers are in the Hot Slots Casino?
B.What is the long run average percentage of these gamblers who
will be at Hot Slots Casino?
casino any of the group members who wish to try their luck at the other casino.The transition probabilities are as follows:
A.After three hours, what proportion of these gamblers are in the Hot Slots Casino?
B.What is the long run average percentage of these gamblers who
will be at Hot Slots Casino?

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
48
Define these Excel functions:

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck
49
Is this an identity matrix? Explain your answer.
| 0 1 0 |
| 1 0 0 |
| 0 0 1 |
| 0 1 0 |
| 1 0 0 |
| 0 0 1 |

Unlock Deck
Unlock for access to all 49 flashcards in this deck.
Unlock Deck
k this deck


