Exam 7: Random Variables and Discrete Probability Distributions

Risky Undertaking Suppose you make a $2,000 investment in a risky undertaking.There is a 50% chance that the payoff from the investment will be $5,000, a 20% chance that you will just get your money back, and a 30% chance that you will receive nothing at all from your investment. -{Risky Undertaking Narrative} Find the expected value of the payoff from your investment of $2,000.

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. -{Shopping Outlet Narrative} Find the expected value of the number of stores entered.

The trials in a binomial experiment are ____________________, meaning the outcome of one trial does not affect the outcomes of any other trials.

Which of the following is not a characteristic of a binomial experiment?

Shopping Outlet A shopping outlet estimates the probability distribution of the number of stores shoppers actually enter as shown in the table below. -{Shopping Outlet Narrative} Find the variance and standard deviation of the number of stores entered.

The Poisson distribution is applied to events for which the probability of occurrence over a given span of time, space, or distance is very small.

Mobile Phones Sales After analyzing sales data, the owner of a Mobile Phone store produced the following joint probability distribution of the number of iPhones (X) and Blackberries (Y) sold daily. 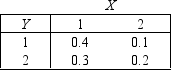-{Mobile Phones Sales Narrative} Calculate E(X + Y) directly by using the probability distribution of X + Y.

Which of the following are required conditions for the distribution of a discrete random variable X that can assume values x_i?

Number of Horses The random variable X represents the number of horses per family in a rural area in Iowa, with the probability distribution: p(x) = 0.05x, x = 2, 3, 4, 5, or 6. -{Number of Horses Narrative} Find the variance and standard deviation of X.

A Poisson random variable is the number of successes that occur in a period of ____________________ or an interval of ____________________ in a Poisson experiment.

Blackjack The probability distribution of a random variable X is shown below, where X represents the amount of money (in $1,000s) gained or lost in a particular game of Blackjack. -{Blackjack Narrative} Find the following probabilities: a. P(X $\le$ 0) b. P(X > 3) c. P(0 $\le$ X $\le$ 4) d. P(X = 5)

A motorcycle insurance company evaluates many numerical variables about a person before deciding on an appropriate rate for motorcycle insurance.The number of tickets a person has received in the last 3 years is an example of a(n) ____________________ random variable.

Number of Birds Alana and Eva are sisters.Let X denote the number of birds that Alana may have in the next two years, and let Y denote the number of birds Eva may have during the same period.The marginal probability distributions of X and Y are shown below. -{Number of Birds Narrative} Compute the covariance between X and Y.

Returns on Investment An analysis of the stock market produces the following information about the returns of two stocks. Assume that the returns are positively correlated with correlation coefficient of 0.80. -{Returns on Investment Narrative} Find the standard deviation of the return on a portfolio consisting of an equal investment in each of the two stocks.

The monthly sales at a Gas Station have a mean of $50,000 and a standard deviation of $6,000.Profits are calculated by multiplying sales by 40% and subtracting fixed costs of $12,000.Find the mean and standard deviation of monthly profits.

The portfolio expected return of two investments:

If X has a binomial distribution with n = 4 and p = 0.3, find the probability that X is at most one.

911 Phone Calls 911 phone calls arrive at the rate of 30 per hour at the local call center. -{911 Phone Calls Narrative} If no calls are currently being processed, what is the probability that the desk employee can take four minutes break without being interrupted?

Car Sales The joint probability distribution of variables X and Y is shown in the table below.Rebecca and Rachel are car salespeople.Let X denote the number of cars that Rebecca will sell in a month, and let Y denote the number of cars Rachel will sell in a month. 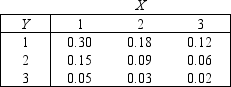-{Car Sales Narrative} Determine the marginal probability distribution of X.

Mobile Phones Sales After analyzing sales data, the owner of a Mobile Phone store produced the following joint probability distribution of the number of iPhones (X) and Blackberries (Y) sold daily. -{Mobile Phones Sales Narrative} Find the marginal probability distribution of the number of iPhones sold daily.