Deck 13: The Integral
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/66
Play
Full screen (f)
Deck 13: The Integral
1
Calculate the Riemann Sum for the integral using n = 4.
A)16
B) 24
C) 30
D) 54
E) 26
A)16
B) 24
C) 30
D) 54
E) 26
30
2
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
Calculate the total area of the region bounded by the line , the x-axis, and the lines and .
A)24,216
B) 966
C) 16,926
D) 50,596
E) 16,744
A)24,216
B) 966
C) 16,926
D) 50,596
E) 16,744
16,926
4
The oxygen consumption of a bird embryo increases from the time the egg is laid through the time the chick hatches. In a typical galliform bird, the oxygen consumption, in milliliters per hour, can be approximated by
where t is time (in days) since the egg was laid. (An egg will typically hatch at around .) Find the total amount of oxygen consumed during the ninth and tenth days ( to ). Round your answer to the nearest whole number.
A)64
B) 18
C) 50
D) 1,138
E) 467
where t is time (in days) since the egg was laid. (An egg will typically hatch at around .) Find the total amount of oxygen consumed during the ninth and tenth days ( to ). Round your answer to the nearest whole number.
A)64
B) 18
C) 50
D) 1,138
E) 467

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
5
Use the given graph to estimate the left Riemann sum for the given interval with the stated number of subdivisions. ![<strong>Use the given graph to estimate the left Riemann sum for the given interval with the stated number of subdivisions. [ 0,3 ] ; n = 3 </strong> A)Left Sum = 1 B) Left Sum = 2 C) Left Sum = - 2 D) Left Sum = 0 E) Left Sum = - 1](https://storage.examlex.com/TB6226/11eb0df5_e66d_666b_9431_fdac73305d6d_TB6226_00.jpg)
A)Left Sum = 1
B) Left Sum = 2
C) Left Sum = - 2
D) Left Sum = 0
E) Left Sum = - 1
![<strong>Use the given graph to estimate the left Riemann sum for the given interval with the stated number of subdivisions. [ 0,3 ] ; n = 3 </strong> A)Left Sum = 1 B) Left Sum = 2 C) Left Sum = - 2 D) Left Sum = 0 E) Left Sum = - 1](https://storage.examlex.com/TB6226/11eb0df5_e66d_666b_9431_fdac73305d6d_TB6226_00.jpg)
A)Left Sum = 1
B) Left Sum = 2
C) Left Sum = - 2
D) Left Sum = 0
E) Left Sum = - 1

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
6
The way Professor Waner drives, he burns gas at the rate of gallons each hour, t hours after a fill-up. Find the number of gallons of gas he burns in the first 13 hours after a fill-up. Please round the answer to the nearest gallon.
A)16 gallons
B) 11 gallons
C) 14 gallons
D) 17 gallons
E) 13 gallons
A)16 gallons
B) 11 gallons
C) 14 gallons
D) 17 gallons
E) 13 gallons

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
7
Evaluate the integral.
A)642
B) 615
C) 18
D) 606
E) 588
A)642
B) 615
C) 18
D) 606
E) 588

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
8
Evaluate the integral.
A)8,272
B) 88
C) 12,056
D) 20,328
E) 3,792
A)8,272
B) 88
C) 12,056
D) 20,328
E) 3,792

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
9
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
10
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
11
A car traveling down a road has a velocity of mph at time ?t hours. Find the total distance it travels from time hours to time hours. (Round your answer to the nearest mile.)
A)216 miles
B) 210 miles
C) 218 miles
D) 224 miles
E) 206 miles
A)216 miles
B) 210 miles
C) 218 miles
D) 224 miles
E) 206 miles

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
12
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
13
Evaluate the integral.
A)38
B) 85.5
C) 10
D) 19
E) 2
A)38
B) 85.5
C) 10
D) 19
E) 2

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
14
Calculate the left Riemann sum for the function over the given interval using the given values of n. over
A)Left Sum = - 5
B) Left Sum = 5
C) Left Sum = 4
D) Left Sum = 7
E) Left Sum = - 4
A)Left Sum = - 5
B) Left Sum = 5
C) Left Sum = 4
D) Left Sum = 7
E) Left Sum = - 4

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
15
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
16
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
17
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
18
Calculate the total area of the region bounded by the line , the x-axis, and the lines and . Round your answer to the nearest whole number.
A)272
B) 833
C) 136
D) 34
E) 17
A)272
B) 833
C) 136
D) 34
E) 17

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
19
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
20
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
21
The rate of change of the total number, in thousand of articles, of research articles in the prominent journal Physics Review written by researchers in Europe is shown in the graph, where t is time in years represents the start of 1983). Use both left and right Riemann sums with 8 subdivisions to estimate the total number of articles in Physics Review written by researchers in Europe in the 16-year period beginning 1983. (Estimate each value of to the nearest 0.5). Use the sums to obtain an estimate of . 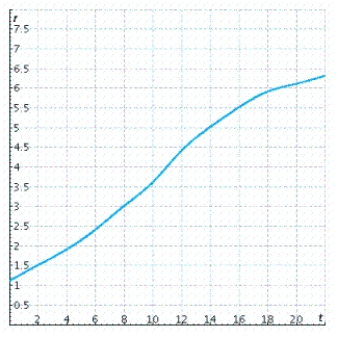
A)9,000 articles
B) 50,500 articles
C) 46,000 articles
D) 4,500 articles
E) 55,000 articles

A)9,000 articles
B) 50,500 articles
C) 46,000 articles
D) 4,500 articles
E) 55,000 articles

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
22
Calculate the left Riemann sums for the function over the given interval, using the given values of n. (When rounding, round answers to four decimal places.)
over
A)Left sum = 0.3548
B) Left sum = 1.7738
C) Left sum = 8.8688
D) Left sum = 0.7095
E) Left sum = 1.4190
over
A)Left sum = 0.3548
B) Left sum = 1.7738
C) Left sum = 8.8688
D) Left sum = 0.7095
E) Left sum = 1.4190

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
23
Decide on what substitution to use, and then evaluate the given integral using a substitution.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
24
Calculate the Riemann Sum for the integral using n = 4.
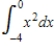
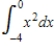

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
25
The normal distribution curve which models, distributions of data in a wide range of applications, is given by the function
where and and are constants called the standard deviation and the mean, respectively. Its graph is shown in the figure.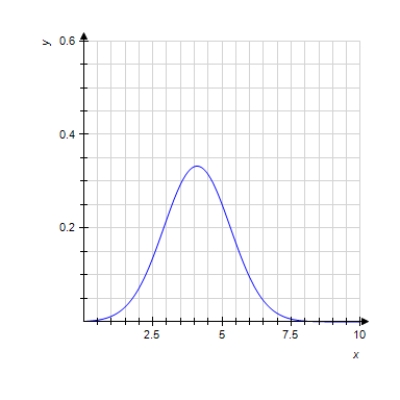 ?
?
In a survey, consumers were asked to rate a new toothpaste on a scale of 1-10. The resulting data are modeled by a normal distribution with and . The percentage of consumers who gave the toothpaste a score between a and b on the section is given by
Use a Riemann sum with n = 10 to estimate the percentage of customers who rated the toothpaste 5 or higher. (Use the range 4.5 to 10.5.) Round your answer to the nearest whole number.
A)45%
B) 46%
C) 47%
D) 48%
E) 49%
where and and are constants called the standard deviation and the mean, respectively. Its graph is shown in the figure.
 ?
?In a survey, consumers were asked to rate a new toothpaste on a scale of 1-10. The resulting data are modeled by a normal distribution with and . The percentage of consumers who gave the toothpaste a score between a and b on the section is given by
Use a Riemann sum with n = 10 to estimate the percentage of customers who rated the toothpaste 5 or higher. (Use the range 4.5 to 10.5.) Round your answer to the nearest whole number.
A)45%
B) 46%
C) 47%
D) 48%
E) 49%

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
26
Evaluate the given integral using the substitution.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
27
Calculate the Riemann Sum for the integral using n = 10.
Round the answer to four decimal places.
A)4,257.7370
B) 5,335.1538
C) 5,261.3439
D) 5,187.5341
E) 42,577.3704
Round the answer to four decimal places.
A)4,257.7370
B) 5,335.1538
C) 5,261.3439
D) 5,187.5341
E) 42,577.3704

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
28
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
29
The graph of the derivative of is shown. Compute the total change of over the interval .
![<strong>The graph of the derivative f ^ { \prime } ( t ) of f ( t ) is shown. Compute the total change of f ( t ) over the interval [ 2,5 ] . </strong> A) f ( 5 ) - f ( 2 ) = 21 B) f ( 5 ) - f ( 2 ) = 7.5 C) f ( 5 ) - f ( 2 ) = 5.25 D) f ( 5 ) - f ( 2 ) = 2.25 E) f ( 5 ) - f ( 2 ) = 10.5](https://storage.examlex.com/TB6226/11eb0df5_e66f_3b3b_9431_b57a498e4d02_TB6226_00.jpg)
A)
B)
C)
D)
E)
![<strong>The graph of the derivative f ^ { \prime } ( t ) of f ( t ) is shown. Compute the total change of f ( t ) over the interval [ 2,5 ] . </strong> A) f ( 5 ) - f ( 2 ) = 21 B) f ( 5 ) - f ( 2 ) = 7.5 C) f ( 5 ) - f ( 2 ) = 5.25 D) f ( 5 ) - f ( 2 ) = 2.25 E) f ( 5 ) - f ( 2 ) = 10.5](https://storage.examlex.com/TB6226/11eb0df5_e66f_3b3b_9431_b57a498e4d02_TB6226_00.jpg)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
30
The marginal cost function for the manufacture of portable CD players is given by
where x is the number of CD players manufactured. Use a Riemann sum with n = 5 to estimate the cost of producing the first 5 CD players. Round your answer to the nearest cent.
A)$249.96
B) $249.95
C) $224.98
D) $249.97
E) $249.98
where x is the number of CD players manufactured. Use a Riemann sum with n = 5 to estimate the cost of producing the first 5 CD players. Round your answer to the nearest cent.
A)$249.96
B) $249.95
C) $224.98
D) $249.97
E) $249.98

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
31
Calculate the Riemann Sum for the integral using .
Round to the nearest tenth.
A) 1.1
B) 1
C) 1.3
D) 2.1
E) 2.5
Round to the nearest tenth.
A) 1.1
B) 1
C) 1.3
D) 2.1
E) 2.5

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
32
A model rocket has upward velocity , t seconds after launch. Use a Riemann sum with n = 10 to estimate how high the rocket is 4 seconds after launch.
A)1094.4 feet
B) 921.6 feet
C) 1478.4 feet
D) 1267.2 feet
E) 960 feet
A)1094.4 feet
B) 921.6 feet
C) 1478.4 feet
D) 1267.2 feet
E) 960 feet

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
33
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
34
A race car has a velocity of , t seconds after starting. Use a Riemann sum with n = 10 to estimate how far the car travels in the first 2 seconds. (Round your answer to the nearest whole number.)
A)780 feet
B) 713 feet
C) 895 feet
D) 576 feet
E) 846 feet
A)780 feet
B) 713 feet
C) 895 feet
D) 576 feet
E) 846 feet

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
35
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
36
Calculate the Riemann Sum for the integral using n = 5. Round your answers to the two decimal places.
A)156.19
B) 468.57
C) 148.41
D) 7.78
E) 23.33
A)156.19
B) 468.57
C) 148.41
D) 7.78
E) 23.33

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
37
Calculate the Riemann Sum for the integral using n = 5.
?
Give the answer correct to two decimal places.
A)0.33
B) 0.81
C) 0.68
D) 0.65
E) 0.53
?
Give the answer correct to two decimal places.
A)0.33
B) 0.81
C) 0.68
D) 0.65
E) 0.53

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
38
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
39
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
40
Calculate the left Riemann sums for the function over the given interval, using the given values of n. (When rounding, round answers to four decimal places.) over
A)Left sum = 343.2693
B) Left sum = 171.6346
C) Left sum = 1,716.3464
D) Left sum = 46.4564
E) Left sum = 34.3269
A)Left sum = 343.2693
B) Left sum = 171.6346
C) Left sum = 1,716.3464
D) Left sum = 46.4564
E) Left sum = 34.3269

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
41
Evaluate the integral. ? ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
42
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
43
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
44
Find if and the tangent line at has the slope .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
45
Find if and the tangent line at has the slope .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
46
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
47
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
48
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
49
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
50
The velocity of a particle moving in a straight line is given by .
Given that the distance at , find an expression for s in terms of t without any unknown constants.
A)
B)
C)
D)
E)
Given that the distance at , find an expression for s in terms of t without any unknown constants.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
51
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
52
Evaluate the integral.
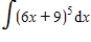
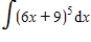

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
53
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
54
The marginal cost of producing the xth roll of film is given by .
The total cost to produce one roll is $700. Find the total cost function .
A)
B)
C)
D)
E)
The total cost to produce one roll is $700. Find the total cost function .
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
55
The velocity of a particle moving in a straight line is given by .
Find an expression for the position s after time t.
A)
B)
C)
D)
E)
Find an expression for the position s after time t.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
56
Evaluate the integral.
A)
B)
C)
D) 1
E)
A)
B)
C)
D) 1
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
57
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
58
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
59
Evaluate the integral mentally.
A)
B)
C) 0
D)
E)
A)
B)
C) 0
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
60
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
61
The marginal cost of producing the xth box of computer disks is and the fixed cost is $120,000. Find the cost function .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
62
Find if and the tangent line at has slope x. ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
63
Find if and the tangent line at has slope . ?
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
64
Evaluate the integral.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
65
Your name is Francesca Dragonetti (an assistant of Galileo Galilei) and, to impress your boss, you toss a weight upward at 32 feet per second from the top of the Leaning Tower of Pisa (height 185 ft). Neglecting air resistance, find the weight's velocity and the height of the weight above the ground as a functions of time in seconds. ?
A) ,
B) ,
C) ,
D) ,
E) ,
A) ,
B) ,
C) ,
D) ,
E) ,

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck
66
The velocity of a particle moving in a straight line is given by .
Find an expression for the position s after a time t.
A)
B)
C)
D)
E)
Find an expression for the position s after a time t.
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 66 flashcards in this deck.
Unlock Deck
k this deck


