Exam 13: The Integral
Exam 1: Functions and Applications159 Questions
Exam 2: Nonlinear Functions and Models92 Questions
Exam 3: The Mathematics of Finance137 Questions
Exam 4: Systems of Linear Equations and Matrices111 Questions
Exam 5: Matrix Algebra and Applications174 Questions
Exam 6: Linear Programming161 Questions
Exam 7: Sets and Counting154 Questions
Exam 8: Probability257 Questions
Exam 9: Random Variables and Statistics178 Questions
Exam 10: Introduction to the Derivative139 Questions
Exam 11: Techniques of Differentiation104 Questions
Exam 12: Applications of the Derivative88 Questions
Exam 13: The Integral66 Questions
Exam 14: Further Integration Techniques and Applications of the Integral118 Questions
Exam 15: Functions of Several Variables137 Questions
Exam 16: Trigonometric Models67 Questions
Select questions type
The marginal cost of producing the xth box of computer disks is and the fixed cost is $120,000. Find the cost function .
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
B
Find if and the tangent line at has slope . ?
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
D
Calculate the left Riemann sums for the function over the given interval, using the given values of n. (When rounding, round answers to four decimal places.)
over
Free
(Multiple Choice)
4.9/5  (39)
(39)
Correct Answer:
D
The rate of change of the total number, in thousand of articles, of research articles in the prominent journal Physics Review written by researchers in Europe is shown in the graph, where t is time in years represents the start of 1983). Use both left and right Riemann sums with 8 subdivisions to estimate the total number of articles in Physics Review written by researchers in Europe in the 16-year period beginning 1983. (Estimate each value of to the nearest 0.5). Use the sums to obtain an estimate of . 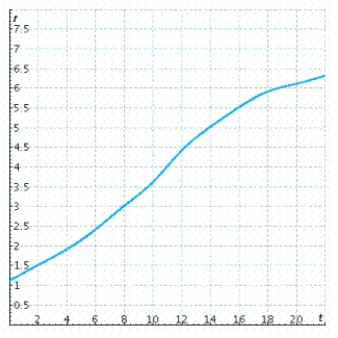
(Multiple Choice)
4.9/5  (40)
(40)
The way Professor Waner drives, he burns gas at the rate of gallons each hour, t hours after a fill-up. Find the number of gallons of gas he burns in the first 13 hours after a fill-up. Please round the answer to the nearest gallon.
(Multiple Choice)
5.0/5  (36)
(36)
Calculate the left Riemann sum for the function over the given interval using the given values of n. over
(Multiple Choice)
4.8/5  (34)
(34)
Calculate the Riemann Sum for the integral using n = 5.
?
Give the answer correct to two decimal places.
(Multiple Choice)
4.9/5  (31)
(31)
Calculate the left Riemann sums for the function over the given interval, using the given values of n. (When rounding, round answers to four decimal places.) over
(Multiple Choice)
4.9/5  (37)
(37)
The velocity of a particle moving in a straight line is given by .
Find an expression for the position s after a time t.
(Multiple Choice)
4.8/5  (32)
(32)
A car traveling down a road has a velocity of mph at time ?t hours. Find the total distance it travels from time hours to time hours. (Round your answer to the nearest mile.)
(Multiple Choice)
4.8/5  (34)
(34)
A model rocket has upward velocity , t seconds after launch. Use a Riemann sum with n = 10 to estimate how high the rocket is 4 seconds after launch.
(Multiple Choice)
4.9/5  (46)
(46)
Calculate the total area of the region bounded by the line , the x-axis, and the lines and .
(Multiple Choice)
4.9/5  (41)
(41)
The velocity of a particle moving in a straight line is given by .
Given that the distance at , find an expression for s in terms of t without any unknown constants.
(Multiple Choice)
4.8/5  (31)
(31)
Showing 1 - 20 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)