Deck 18: Simple Linear Regression and Correlation
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/219
Play
Full screen (f)
Deck 18: Simple Linear Regression and Correlation
1
Which of the following best describes the relationship of the least squares regression line: Estimated y = 2 - x? 

C
2
The regression line Estimated y = 3 + 2x has been fitted to the data points (4,8), (2,5), and (1,2). The sum of the squared residuals will be: 

D
3
Which of the following statements best describes correlation analysis in a simple linear regression? 

B
4
Given a specific value of x and confidence level, which of the following statements is correct? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
5
If an estimated regression line has a y-intercept of 10 and a slope of -5, then when x = 0, the estimated value of y is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
6
Given that the sum of squares for error is 50 and the sum of squares for regression is 140, the coefficient of determination is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
7
The Spearman rank correlation coefficient must be used to determine whether a relationship exists between two variables when: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
8
The symbol for the population coefficient of correlation is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
9
If the coefficient of correlation is 0.80, the percentage of the variation in y that is explained by the variation in x is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
10
In regression analysis, if the coefficient of determination is 1.0, then: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
11
Given the least squares regression line y-hat = 3.52 - 1.27x, and a coefficient of determination of 0.81, the coefficient of correlation is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
12
A regression line using 25 observations produced SSR = 118.68 and SSE = 56.32. The standard error of estimate was: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
13
Given that ssx = 2500, ssy = 3750, ssxy = 500 and n = 6, the standard error of estimate is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
14
The following sums of squares are produced: (yi-(y-bar))2 = 250, (yi-(yi-hat))2 = 100, ((yi-hat)-(y-bar))2 = 150
The percentage of the variation in y that is explained by the variation in x is:
The percentage of the variation in y that is explained by the variation in x is:

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following best describes the value of the slope, if the coefficient of determination is 0.95? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
16
In simple linear regression, most often we perform a two-tail test of the population slope 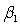 to determine whether there is sufficient evidence to infer that a linear relationship exists. Which of the following best describes the null and alternative hypotheses needed for a test of significance?
to determine whether there is sufficient evidence to infer that a linear relationship exists. Which of the following best describes the null and alternative hypotheses needed for a test of significance? 
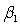 to determine whether there is sufficient evidence to infer that a linear relationship exists. Which of the following best describes the null and alternative hypotheses needed for a test of significance?
to determine whether there is sufficient evidence to infer that a linear relationship exists. Which of the following best describes the null and alternative hypotheses needed for a test of significance? 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
17
If the coefficient of correlation is −0.50, the percentage of the variation in the dependent variable y that is explained by the variation in the independent variable x is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
18
In a simple linear regression, which of the following is equivalent to testing the significance of the population slope? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
19
The symbol for the sample coefficient of correlation is: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
20
Which value of the coefficient of correlation r indicates a stronger correlation than − 0.85? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
21
A regression analysis between sales (in $1000) and advertising (in $100) yielded the least squares line 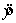 = 75 +6x. This implies that if $800 is spent on advertising, then the predicted amount of sales (in dollars) is:
= 75 +6x. This implies that if $800 is spent on advertising, then the predicted amount of sales (in dollars) is: 
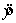 = 75 +6x. This implies that if $800 is spent on advertising, then the predicted amount of sales (in dollars) is:
= 75 +6x. This implies that if $800 is spent on advertising, then the predicted amount of sales (in dollars) is: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
22
The smallest value that the standard error of estimate 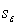 can assume is:
can assume is: 
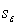 can assume is:
can assume is: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
23
If all the points in a scatter diagram lie on the least squares regression line, then the coefficient of correlation must be: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
24
Given the data points (x,y) = (3,3), (4,4), (5,5), (6,6), (7,7), the least squares estimates of the y-intercept and slope are respectively: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
25
Of the values of the coefficient of determination listed below, which one implies the greatest value of the sum of squares for regression, given that the total variation in y is 1800? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
26
When all the actual values of y and the predicted values of y are equal, the standard error of estimate will be: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
27
In order to estimate with 95% confidence the expected value of y in a simple linear regression problem, a random sample of 10 observations is taken. Which of the following t-table values listed below would be used? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
28
A regression analysis between sales (in $1000) and advertising (in $) yielded the least squares line 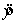 = 80 000 + 5x. This implies that an:
= 80 000 + 5x. This implies that an: 
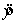 = 80 000 + 5x. This implies that an:
= 80 000 + 5x. This implies that an: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
29
If the coefficient of correlation between x and y is close to −1.0, which of the following statements is correct? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
30
Which of the following techniques is used to predict the value of one variable on the basis of other variables? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
31
In testing the hypotheses: 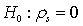
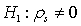 , the Spearman rank correlation coefficient in a sample of 50 observations is 0.389. The value of the test statistic is:
, the Spearman rank correlation coefficient in a sample of 50 observations is 0.389. The value of the test statistic is: 
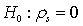
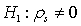 , the Spearman rank correlation coefficient in a sample of 50 observations is 0.389. The value of the test statistic is:
, the Spearman rank correlation coefficient in a sample of 50 observations is 0.389. The value of the test statistic is: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
32
Which of the following statements best describes why a linear regression is also called a least squares regression model? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
33
If the standard error of estimate 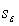 = 15 and n = 12, then the sum of squares for error, SSE, is:
= 15 and n = 12, then the sum of squares for error, SSE, is: 
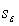 = 15 and n = 12, then the sum of squares for error, SSE, is:
= 15 and n = 12, then the sum of squares for error, SSE, is: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
34
A regression analysis between height y (in cm) and age x (in years) of 2 to 10 years old boys yielded the least squares line y-hat = 87 + 6.5x. This implies that by each additional year height is expected to: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
35
Which of the following statistics and procedures can be used to determine whether a linear model should be employed? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
36
In regression analysis, if the coefficient of correlation is -1.0, then: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
37
The standardised residual is defined as: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
38
If the coefficient of determination is 81%, and the linear regression model has a negative slope, what is the value of the coefficient of correlation? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
39
Which of the following statements is correct when all the actual values of y are on an upward sloping regression line? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
40
The standard error of estimate, 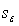 , is given by:
, is given by: 
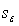 , is given by:
, is given by: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
41
In regression analysis, the coefficient of determination, 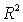 , measures the amount of variation in y that is:
, measures the amount of variation in y that is: 
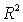 , measures the amount of variation in y that is:
, measures the amount of variation in y that is: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
42
If cov(X,Y) = -350, sx2 = 900 and sy2 = 225, then the coefficient of determination is:

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
43
When the variance, 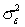 , of the error variable
, of the error variable 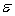 is a constant no matter what the value of x is, this condition is called:
is a constant no matter what the value of x is, this condition is called: 
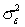 , of the error variable
, of the error variable 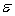 is a constant no matter what the value of x is, this condition is called:
is a constant no matter what the value of x is, this condition is called: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
44
The standard error of estimate, 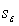 , is a measure of:
, is a measure of: 
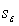 , is a measure of:
, is a measure of: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
45
Which of the following statements best describes the slope in the simple linear regression model? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
46
Which of the following best describes the y-intercept in the simple linear regression model? 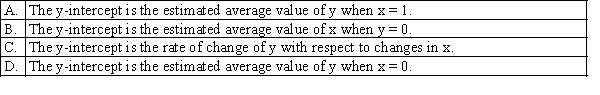
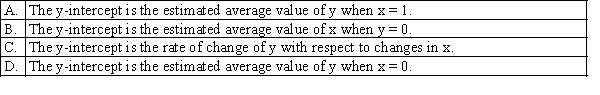

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
47
Which of the following best describes if we want to test for a linear relationship between x and y, in regression analysis? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
48
In the first-order linear regression model, the population parameters of the y-intercept and the slope are: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
49
In a regression problem the following pairs (x,y) are given: (1,2), (2.5,2), (3,2), (5,2) and (5.3,2). This indicates that the: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
50
Which of the following is not a required condition for the error variable 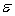 in the simple linear regression model?
in the simple linear regression model? 
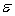 in the simple linear regression model?
in the simple linear regression model? 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
51
In simple linear regression, the coefficient of correlation r and the least squares estimate 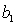 of the population slope
of the population slope 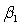 :
: 
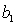 of the population slope
of the population slope 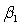 :
: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
52
When the sample size n is greater than 30, the Spearman rank correlation coefficient 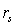 is approximately normally distributed with:
is approximately normally distributed with: 
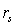 is approximately normally distributed with:
is approximately normally distributed with: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
53
The least squares method requires that the variance 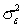 of the error variable
of the error variable  is a constant no matter what the value of x is. When this requirement is violated, the condition is called:
is a constant no matter what the value of x is. When this requirement is violated, the condition is called: 
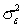 of the error variable
of the error variable  is a constant no matter what the value of x is. When this requirement is violated, the condition is called:
is a constant no matter what the value of x is. When this requirement is violated, the condition is called: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
54
In the first-order linear regression model, the population parameters of the y-intercept and the slope are estimated by: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
55
Which of the following best describes the coefficient of determination? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
56
In a regression problem, if the coefficient of determination is 0.95, this means that: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
57
Which of the following best describes the residuals in regression analysis? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
58
If a simple linear regression model has no y-intercept, then: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
59
In a simple linear regression problem, the following statistics are calculated from a sample of 10 observations: 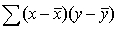 = 2250,
= 2250, 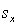 = 10,
= 10, 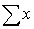 = 50,
= 50, 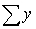 = 75 The least squares estimates of the slope and y-intercept are respectively:
= 75 The least squares estimates of the slope and y-intercept are respectively: 
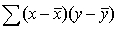 = 2250,
= 2250, 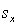 = 10,
= 10, 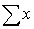 = 50,
= 50, 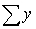 = 75 The least squares estimates of the slope and y-intercept are respectively:
= 75 The least squares estimates of the slope and y-intercept are respectively: 

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
60
The Pearson coefficient of correlation r equals 1 when there is/are no: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
61
The value of the sum of squares for regression, SSR, can never be smaller than 0.0.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
62
In developing a 90% confidence interval for the expected value of y from a simple linear regression problem involving a sample of size 15, the appropriate table value would be 1.761.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
63
Regardless of the value of x, the standard deviation of the distribution of y values about the regression line is supposed to be constant. This assumption of equal standard deviations about the regression line is called multicollinearity.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
64
The variance of the error variable, , is required to be constant. When this requirement is satisfied, the condition is called homoscedasticity.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
65
If all the values of an independent variable x are equal, then regressing a dependent variable y on x will result in a coefficient of determination of 100%.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
66
The method of least squares requires that the sum of the squared deviations between actual y values in the scatter diagram and y values predicted by the regression line be minimised.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
67
When the actual values y of a dependent variable and the corresponding predicted values 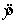 are the same, the standard error of the estimate will be 1.0.
are the same, the standard error of the estimate will be 1.0.
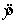 are the same, the standard error of the estimate will be 1.0.
are the same, the standard error of the estimate will be 1.0.
Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
68
If the sum of squared residuals is zero, then the: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
69
The least squares method for determining the best fit minimises: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
70
In a simple linear regression model, testing whether the slope, , of the population regression line is zero is the same as testing whether the population coefficient of correlation, , equals zero.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
71
The variance of the error variable, , is required to be constant. When this requirement is violated, the condition is called heteroscedasticity.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
72
In a regression problem, if all the values of the independent variable are equal, then the coefficient of determination must be: 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
73
In developing a 95% confidence interval for the expected value of y from a simple linear regression problem involving a sample of size 10, the appropriate table value would be 2.306.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
74
The value of the sum of squares for regression, SSR, can never be smaller than 1.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
75
A direct relationship between an independent variable x and a dependent variably y means that x and y move in the same directions.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
76
A direct relationship between an independent variable x and a dependent variably y means that the variables x and y increase or decrease together.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
77
If the value of the sum of squares for error, SSE, equals zero, then the coefficient of determination must equal zero.

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
78
On the least squares regression line Estimated y= 2 - 3x, the predicted value of y equals:

Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
79
When the actual values y of a dependent variable and the corresponding predicted values 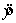 are the same, the standard error of estimate, , will be 0.0.
are the same, the standard error of estimate, , will be 0.0.
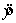 are the same, the standard error of estimate, , will be 0.0.
are the same, the standard error of estimate, , will be 0.0. 
Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck
80
In simple linear regression, which of the following statements indicates no linear relationship between the variables x and y? 


Unlock Deck
Unlock for access to all 219 flashcards in this deck.
Unlock Deck
k this deck


