Deck 15: Optimization- Local and Global Extrema
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/77
Play
Full screen (f)
Deck 15: Optimization- Local and Global Extrema
1
Suppose that Find an equation of the tangent plane to the graph of f at the point (2, 2).
A)
B)
C)
D)
A)
B)
C)
D)
2
Let 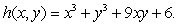 Determine all local maxima, minima, and saddle points.Are the local extrema also global extrema?
Determine all local maxima, minima, and saddle points.Are the local extrema also global extrema?
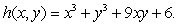 Determine all local maxima, minima, and saddle points.Are the local extrema also global extrema?
Determine all local maxima, minima, and saddle points.Are the local extrema also global extrema?(0, 0)is a saddle point; (-3, -3)is a local maximum.There is no global extremum.
3
Find the critical points of 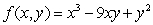 and classify each as maximum, minimum or saddle.
and classify each as maximum, minimum or saddle.
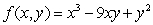 and classify each as maximum, minimum or saddle.
and classify each as maximum, minimum or saddle.The point (0, 0)is a saddle point.
The point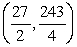 is a local minimum.
is a local minimum.
The point
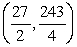 is a local minimum.
is a local minimum. 4
Level curves of f(x, y)are shown in the figure below.(Darker shades indicate regions with lower levels.)
Determine if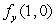 is positive, negative or zero.
is positive, negative or zero. 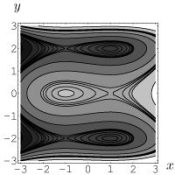
Determine if
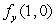 is positive, negative or zero.
is positive, negative or zero. 

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
5
The function has a saddle point at (-1, 12).Which of the following is a sketch of the level curves of f near this point?
A)
B)
A)

B)


Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
6
Level curves of f(x, y)are shown in the figure below.(Darker shades indicate regions with lower levels.) Is the point (-1, 2)a local maximum, a local minimum, or a saddle point of f, or is it none of these? 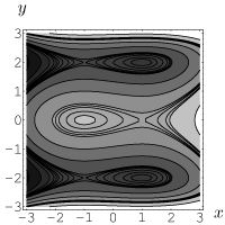
A)Saddle point.
B)Local minimum.
C)Local maximum.
D)None of these.

A)Saddle point.
B)Local minimum.
C)Local maximum.
D)None of these.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
7
Consider the function 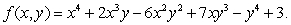 Check that (0,0)is a critical point of f and classify it as a local minimum, local maximum or saddle point.
Check that (0,0)is a critical point of f and classify it as a local minimum, local maximum or saddle point.
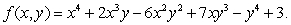 Check that (0,0)is a critical point of f and classify it as a local minimum, local maximum or saddle point.
Check that (0,0)is a critical point of f and classify it as a local minimum, local maximum or saddle point.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
8
Let Which figure best represents the level curves of this function?
A)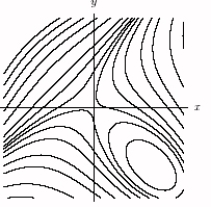
B)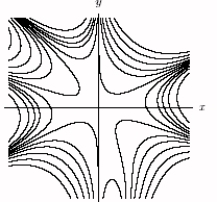
C)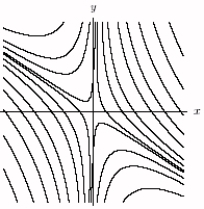
D)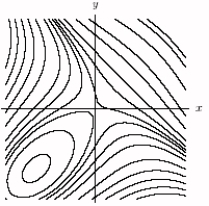
A)

B)

C)

D)


Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
9
The function f(x, y)has a local maximum at (-1, 1). What can you say (if anything)about the values of ?
A)Nothing.
B)It is undefined or equal to zero.
C)It cannot be greater than zero.
D)It is equal to zero.
A)Nothing.
B)It is undefined or equal to zero.
C)It cannot be greater than zero.
D)It is equal to zero.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
10
The contour diagram of f is shown below. 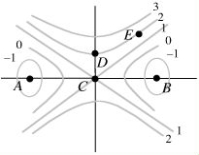 Find and classify the critical points.
Find and classify the critical points.
Describe possible gradient vectors of f at points C, D and E.
 Find and classify the critical points.
Find and classify the critical points.Describe possible gradient vectors of f at points C, D and E.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose that 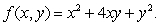 Find and classify the critical point(s)as local maxima, local minima, or saddle points.
Find and classify the critical point(s)as local maxima, local minima, or saddle points.
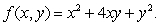 Find and classify the critical point(s)as local maxima, local minima, or saddle points.
Find and classify the critical point(s)as local maxima, local minima, or saddle points.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
12
Let , where a, b are any numbers with a 2.
Find the critical point of f.(Express your answer in terms of the constants a and b.)
Find the critical point of f.(Express your answer in terms of the constants a and b.)

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
13
Is (0, 0)a critical point of the following function?
A)No.
B)Yes: (global)maximum.
C)Yes: local minimum.
D)Yes: (global)minimum.
A)No.
B)Yes: (global)maximum.
C)Yes: local minimum.
D)Yes: (global)minimum.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
14
Find all the critical points of and classify each as maximum, minimum, or saddle point. Select all possible choices.
A)The point (1, 2)is a relative minimum.
B)The point (-1, -2)is a saddle point.
C)The point (-1, 2)is a saddle point.
D)The point (1, 2)is a relative maximum.
E)The point (1, -2)is a relative maximum.
A)The point (1, 2)is a relative minimum.
B)The point (-1, -2)is a saddle point.
C)The point (-1, 2)is a saddle point.
D)The point (1, 2)is a relative maximum.
E)The point (1, -2)is a relative maximum.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose that Find a normal vector to the tangent plane of f at the point (1, 1).Select all that apply.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
16
Let , where a, b are any positive numbers with a 4.
Find the minimum value of a such that the critical point will be a saddle point.
Find the minimum value of a such that the critical point will be a saddle point.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
17
The contour diagram of f is shown below.Which of the points A, B, C, D, and E appear to be critical points? Select all that apply. 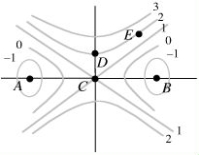
A)A
B)B
C)C
D)D
E)E

A)A
B)B
C)C
D)D
E)E

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
18
Suppose that (1, -4)is a critical point of a smooth function f(x, y)with 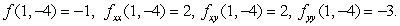 Find the quadratic approximation of f at (1, -4).
Find the quadratic approximation of f at (1, -4).
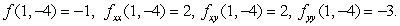 Find the quadratic approximation of f at (1, -4).
Find the quadratic approximation of f at (1, -4).
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
19
Suppose that (0, -2)is a critical point of a smooth function f(x, y)with 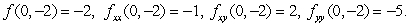 What can you conclude about the behavior of the function f near (0, -2)?
What can you conclude about the behavior of the function f near (0, -2)?
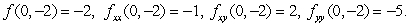 What can you conclude about the behavior of the function f near (0, -2)?
What can you conclude about the behavior of the function f near (0, -2)?
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
20
Find all the critical points of the function 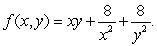 Classify these critical points as local maxima, local minima, or saddle points.
Classify these critical points as local maxima, local minima, or saddle points.
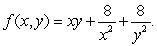 Classify these critical points as local maxima, local minima, or saddle points.
Classify these critical points as local maxima, local minima, or saddle points.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
21
Determine the nature of the critical points of the function
A)f has a saddle point at (1, 0).
B)f has a local maximum at (0, 0).
C)f has a saddle point at (0, 1).
D)f has a saddle point at (0, 0).
E)f has a local minimum at (0, 0).
A)f has a saddle point at (1, 0).
B)f has a local maximum at (0, 0).
C)f has a saddle point at (0, 1).
D)f has a saddle point at (0, 0).
E)f has a local minimum at (0, 0).

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the four points A = (1, 0), B = (2, 3), C = (3, 5)and D = (4, 3)in the xy-plane.
Find the values of a, b and c to determine the parabola of best fit,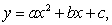 for these points.
for these points.
(The parabola of best fit minimizes the sum of the squares of the vertical distances from each point to the parabola.)
Find the values of a, b and c to determine the parabola of best fit,
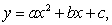 for these points.
for these points.(The parabola of best fit minimizes the sum of the squares of the vertical distances from each point to the parabola.)

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the four points A = (1, 0), B = (2, 2), C = (3, 5)and D = (4, 3)in the xy-plane.
Find a and b in the line of best fit y = ax + b for these points.
(The line of best fit minimizes the sum of the squares of the vertical distances from each point to the line.)
Find a and b in the line of best fit y = ax + b for these points.
(The line of best fit minimizes the sum of the squares of the vertical distances from each point to the line.)

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
24
Consider the diagram shown below, which shows gradient vectors of a function f(x, y). 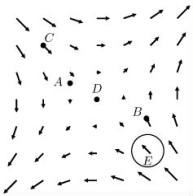 Which is less: f(A)or f(C)?
Which is less: f(A)or f(C)?
 Which is less: f(A)or f(C)?
Which is less: f(A)or f(C)?
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
25
The point (-2, 1)is a critical point of 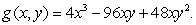 Classify it either as a local minimum, local maximum, or saddle point.
Classify it either as a local minimum, local maximum, or saddle point.
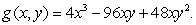 Classify it either as a local minimum, local maximum, or saddle point.
Classify it either as a local minimum, local maximum, or saddle point.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
26
Suppose that 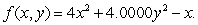 Find and classify (as local maxima, minima, or saddle points)all critical points of f.
Find and classify (as local maxima, minima, or saddle points)all critical points of f.
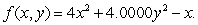 Find and classify (as local maxima, minima, or saddle points)all critical points of f.
Find and classify (as local maxima, minima, or saddle points)all critical points of f.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
27
Without calculating the discriminant, explain using the contour diagram for 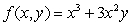 why f has a saddle point at (0, 0).
why f has a saddle point at (0, 0). 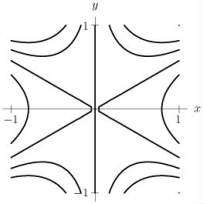
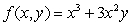 why f has a saddle point at (0, 0).
why f has a saddle point at (0, 0). 

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
28
Find the critical points of 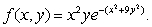 Do this by setting
Do this by setting 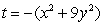 and optimizing
and optimizing 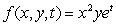 subject to the constraint
subject to the constraint 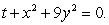
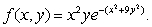 Do this by setting
Do this by setting 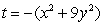 and optimizing
and optimizing 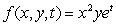 subject to the constraint
subject to the constraint 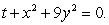

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
29
What do the second derivatives tell you about the graph of Select all that apply.
A)Any critical point must be a saddle point.
B)There is a local minimum.
C)There are no local minima.
D)The function has a local maximum.
E)There are at least two local minima.
A)Any critical point must be a saddle point.
B)There is a local minimum.
C)There are no local minima.
D)The function has a local maximum.
E)There are at least two local minima.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
30
Find a and b so that 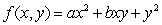 has a critical point at (1, 6).
has a critical point at (1, 6).
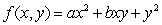 has a critical point at (1, 6).
has a critical point at (1, 6).
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
31
The function 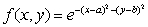 where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points.Show that f(x, y)has a maximum at (a, b).
where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points.Show that f(x, y)has a maximum at (a, b).
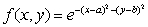 where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points.Show that f(x, y)has a maximum at (a, b).
where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points.Show that f(x, y)has a maximum at (a, b).
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
32
A zoo is designing a giant bird cage consisting of a cylinder of radius r feet and height h feet with a hemisphere on top (no bottom).The material for the hemisphere costs $20 per square foot and the material for the cylindrical sides costs $10 per square foot; the zoo has a budget of $5120.Find the values of r and h giving the birds the greatest space inside assuming the zoo stays within its budget.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
33
Consider the function 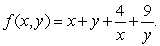 Determine all the local maximum, minimum and saddle points in the region
Determine all the local maximum, minimum and saddle points in the region 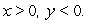
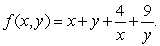 Determine all the local maximum, minimum and saddle points in the region
Determine all the local maximum, minimum and saddle points in the region 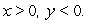

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
34
Find the critical point of 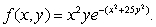 Do this by setting
Do this by setting 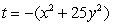 and optimizing
and optimizing 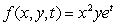 subject to the constraint
subject to the constraint 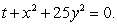 What are the global maximum and minimum values of f? Give your answer to 4 decimal places.
What are the global maximum and minimum values of f? Give your answer to 4 decimal places.
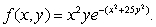 Do this by setting
Do this by setting 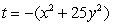 and optimizing
and optimizing 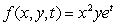 subject to the constraint
subject to the constraint 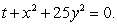 What are the global maximum and minimum values of f? Give your answer to 4 decimal places.
What are the global maximum and minimum values of f? Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
35
The Perfect House company produces two types of bathtub, the Hydro Deluxe model and the Singing Bird model.The company noticed that demand and prices are related.In particular,
for Hydro Deluxe: demand = 1900 - price of Hydro Deluxe + price of Singing Bird
for Singing Bird: demand = 1450 + price of Hydro Deluxe -2(price of Singing Bird).
The costs of manufacturing the Hydro Deluxe and Singing Bird are $500 and $300 per unit respectively.Determine the price of each model that gives the maximum profit.
for Hydro Deluxe: demand = 1900 - price of Hydro Deluxe + price of Singing Bird
for Singing Bird: demand = 1450 + price of Hydro Deluxe -2(price of Singing Bird).
The costs of manufacturing the Hydro Deluxe and Singing Bird are $500 and $300 per unit respectively.Determine the price of each model that gives the maximum profit.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
36
Find a point on the surface x-yz = 14 that is closest to the origin.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
37
If C is a circle in the plane, and if f(x, y)is differentiable and is not constant when constrained to C, then there must be at least one point on C where is perpendicular to C.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
38
Describe the shape of the graph of
A)Paraboloid
B)Elliptic paraboloid
C)Hyperbolic paraboloid
D)None of the above
A)Paraboloid
B)Elliptic paraboloid
C)Hyperbolic paraboloid
D)None of the above

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
39
A company has $250,000 to spend on labor and raw materials.Let L be the quantity of labor and R be the quantity of raw materials.The production output P of the company is cRL (here c is a positive constant).Suppose that each unit of labor costs $6000 and the unit price of raw materials is $2000.
Find the ratio of R to L that maximizes P.
Find the ratio of R to L that maximizes P.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
40
A company has two manufacturing plants which manufacture the same item.Suppose the cost function is given by 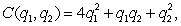 where q1 and q2 are the quantities (measured in thousands)produced in each plant.The total demand q1 + q2 is related to the price, p, by
where q1 and q2 are the quantities (measured in thousands)produced in each plant.The total demand q1 + q2 is related to the price, p, by 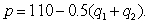 How much should each plant produce in order to maximize the company's profit?
How much should each plant produce in order to maximize the company's profit?
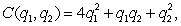 where q1 and q2 are the quantities (measured in thousands)produced in each plant.The total demand q1 + q2 is related to the price, p, by
where q1 and q2 are the quantities (measured in thousands)produced in each plant.The total demand q1 + q2 is related to the price, p, by 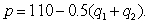 How much should each plant produce in order to maximize the company's profit?
How much should each plant produce in order to maximize the company's profit?
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
41
(a)Let .Find the maximum and minimum values of f on the curve
(b)Use the results of part (a)to find the maximum and minimum values of on the curve Explain your work.
(b)Use the results of part (a)to find the maximum and minimum values of on the curve Explain your work.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
42
The owner of a jewelry store has to decide how to allocate a budget of $540,000.He notices that the earnings of the company depend on investment in inventory x1 (in thousands of dollars)and expenditure x2 on advertising (in thousands of dollars)according to the function 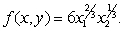 How should the owner allocate the $540,000 between inventory and advertising to maximize his profit?
How should the owner allocate the $540,000 between inventory and advertising to maximize his profit?
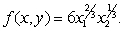 How should the owner allocate the $540,000 between inventory and advertising to maximize his profit?
How should the owner allocate the $540,000 between inventory and advertising to maximize his profit?
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
43
Find the saddle point of 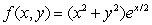 .
.
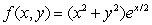 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
44
Suppose that you want to find the maximum and minimum values of 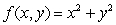 subject to the constraint x + 4y = 3.
subject to the constraint x + 4y = 3.
Use the method of Lagrange multipliers to find the exact location(s)of any extrema.
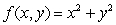 subject to the constraint x + 4y = 3.
subject to the constraint x + 4y = 3.Use the method of Lagrange multipliers to find the exact location(s)of any extrema.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
45
Determine three positive numbers x, y, z that maximize 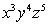 under the condition x + y + z = 17.
under the condition x + y + z = 17.
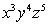 under the condition x + y + z = 17.
under the condition x + y + z = 17.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
46
Consider the function 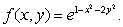 Determine all local maxima, minima and saddle points of f.
Determine all local maxima, minima and saddle points of f.
Does f have a global maximum?
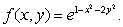 Determine all local maxima, minima and saddle points of f.
Determine all local maxima, minima and saddle points of f.Does f have a global maximum?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
47
Find the maximum and minimum values of the function 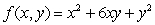 subject to the constraint
subject to the constraint 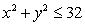 .
.
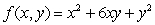 subject to the constraint
subject to the constraint 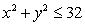 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose the quantity, q, of a good produced depends on the number of workers, w, and the amount of capital, k, invested and is represented by the Cobb-Douglas function 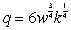 .In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $3680.Using Lagrange multipliers, find the optimum number of units of capital.
.In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $3680.Using Lagrange multipliers, find the optimum number of units of capital.
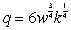 .In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $3680.Using Lagrange multipliers, find the optimum number of units of capital.
.In addition, labor costs are $20 per worker and capital costs are $20 per unit, and the budget is $3680.Using Lagrange multipliers, find the optimum number of units of capital.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
49
A company manufactures a product using x, y and z units of three different raw materials.The quantity produced is given by the function 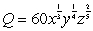 .Suppose the cost of the materials per unit is $20, $25 and $75 respectively.
.Suppose the cost of the materials per unit is $20, $25 and $75 respectively.
Find the maximum production if the budget is limited to $6000.
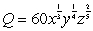 .Suppose the cost of the materials per unit is $20, $25 and $75 respectively.
.Suppose the cost of the materials per unit is $20, $25 and $75 respectively.Find the maximum production if the budget is limited to $6000.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
50
The Green Leaf Bakery makes two types of chocolate cakes, Delicious and Extra Delicious.Each Delicious requires 0.1 lb of European chocolate, while each Extra Delicious requires 0.2 lb.Currently there are only 233 lb of chocolate available each month.Suppose the profit function is given by: where x is the number of Delicious cakes and y is the number of Extra Delicious cakes that the bakery produces each month.
(a)How many of each cake should the bakery produce each month to maximize profit?
(b)What is the value of in part (a)(if )? What does it mean?
(c)It will cost $19.00 to get an extra pound of European chocolate.Should the bakery buy it?
(a)How many of each cake should the bakery produce each month to maximize profit?
(b)What is the value of in part (a)(if )? What does it mean?
(c)It will cost $19.00 to get an extra pound of European chocolate.Should the bakery buy it?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
51
A coffee company sells three brands of coffee.Brand A costs p1 dollars per can, brand B costs p2 dollars per can, and brand C costs p3 dollars per can.The demand (in hundreds of cans)depends on the prices as follows:
demand for brand A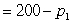 ,
,
demand for brand B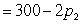 ,
,
demand for brand C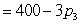 .
.
The company can produce 69,000 cans.What selling prices optimize the total revenue?
demand for brand A
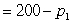 ,
,demand for brand B
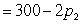 ,
,demand for brand C
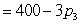 .
.The company can produce 69,000 cans.What selling prices optimize the total revenue?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
52
Suppose that 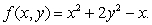 Find the minimum value of the function f when (x,y)is constrained to lie on or inside the triangle with vertices (0,-2), (0,1), and (1,-2).Give your answer to 4 decimal places.
Find the minimum value of the function f when (x,y)is constrained to lie on or inside the triangle with vertices (0,-2), (0,1), and (1,-2).Give your answer to 4 decimal places.
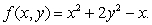 Find the minimum value of the function f when (x,y)is constrained to lie on or inside the triangle with vertices (0,-2), (0,1), and (1,-2).Give your answer to 4 decimal places.
Find the minimum value of the function f when (x,y)is constrained to lie on or inside the triangle with vertices (0,-2), (0,1), and (1,-2).Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
53
The following results are obtained when optimizing f(x, y)subject to the constraint g(x, y)= 35.The maximum value is f(5, 7)= 39, the Lagrange multiplier = 4 (when )and .What is g(5, 7)?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
54
A company manufactures a product using x, y and z units of three different raw materials.The quantity produced is given by The production is described by the function 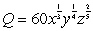 .Suppose the cost of the materials per unit is $20, $15 and $24 respectively.
.Suppose the cost of the materials per unit is $20, $15 and $24 respectively.
(a)Find the cheapest way to produce 6300 units of the product.
(b)Find the value of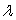 in
in 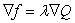 and interpret this value.
and interpret this value.
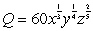 .Suppose the cost of the materials per unit is $20, $15 and $24 respectively.
.Suppose the cost of the materials per unit is $20, $15 and $24 respectively.(a)Find the cheapest way to produce 6300 units of the product.
(b)Find the value of
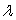 in
in 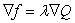 and interpret this value.
and interpret this value.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
55
Use Lagrange multipliers to find the minimum value of 4xy on the circle 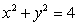 .
.
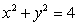 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
56
Let 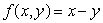 .The constraint g(x, y)= 3 is sketched in the picture below.
.The constraint g(x, y)= 3 is sketched in the picture below.
In the picture, locate the point where f will have a global maximum subject to the constraint g(x, y)= 3.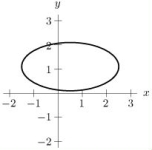
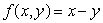 .The constraint g(x, y)= 3 is sketched in the picture below.
.The constraint g(x, y)= 3 is sketched in the picture below.In the picture, locate the point where f will have a global maximum subject to the constraint g(x, y)= 3.


Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
57
The Lagrange multipliers needed to find the maximum and minimum values of 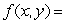 8xy on the circle
8xy on the circle 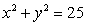 is
is 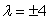 , where
, where 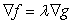 .Estimate the maximum and minimum values of 8xy subject to the constraint
.Estimate the maximum and minimum values of 8xy subject to the constraint 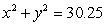 .
.
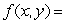 8xy on the circle
8xy on the circle 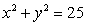 is
is 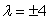 , where
, where 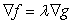 .Estimate the maximum and minimum values of 8xy subject to the constraint
.Estimate the maximum and minimum values of 8xy subject to the constraint 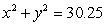 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
58
Given that the quadratic Taylor polynomial of f at (4, 5)is 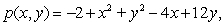 decide whether
decide whether 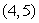 is a critical point.If so, identify what sort of critical point it is.
is a critical point.If so, identify what sort of critical point it is.
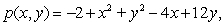 decide whether
decide whether 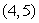 is a critical point.If so, identify what sort of critical point it is.
is a critical point.If so, identify what sort of critical point it is.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
59
The following results are obtained when optimizing f(x, y)subject to the constraint g(x, y)= 39.The maximum value is f(5, 7)= 42, the Lagrange multiplier = 3 (when )and .If the constraint condition is changed to g(x, y)= 40, what will be new maximum value of f(x, y)?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
60
Let 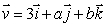 be a vector in space with a, b > 0.
be a vector in space with a, b > 0.
Compute the cross product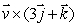 and then use the result and the Lagrange Multiplier method to find the values of a and b such that the magnitude of the cross product
and then use the result and the Lagrange Multiplier method to find the values of a and b such that the magnitude of the cross product 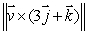 is the largest with
is the largest with 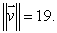
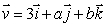 be a vector in space with a, b > 0.
be a vector in space with a, b > 0.Compute the cross product
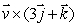 and then use the result and the Lagrange Multiplier method to find the values of a and b such that the magnitude of the cross product
and then use the result and the Lagrange Multiplier method to find the values of a and b such that the magnitude of the cross product 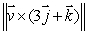 is the largest with
is the largest with 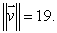

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
61
Let , for constants a, b, c, and d, with .
The constants can be chosen in such a way that f will have a local minimum.
The constants can be chosen in such a way that f will have a local minimum.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
62
Suppose there are two electric generators that burn natural gas and whose efficiency declines with output.The energy output is an increasing (but concave down)function of fuel input.Specifically, say
Output of generator 1 is
Output of generator 1 is

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
63
Let .
There exist values of a and b so that takes a minimum value of 8 on the unit circle at the point .
There exist values of a and b so that takes a minimum value of 8 on the unit circle at the point .

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
64
An exam question asks students to find the maximum of 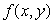 on the circle
on the circle 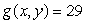 , and the gradient vectors of f and g at that point.A student gave the following
, and the gradient vectors of f and g at that point.A student gave the following
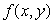 on the circle
on the circle 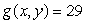 , and the gradient vectors of f and g at that point.A student gave the following
, and the gradient vectors of f and g at that point.A student gave the following
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
65
Find three positive numbers whose product is 11 and whose sum is a minimum.What is the minimum sum?

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
66
Let 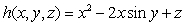 .Let
.Let 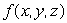 satisfy
satisfy 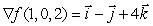 .Explain why the maximum of f subject to the constraint
.Explain why the maximum of f subject to the constraint 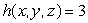 cannot occur at the point
cannot occur at the point 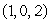 .
.
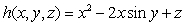 .Let
.Let 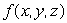 satisfy
satisfy 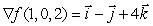 .Explain why the maximum of f subject to the constraint
.Explain why the maximum of f subject to the constraint 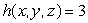 cannot occur at the point
cannot occur at the point 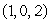 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
67
The point (0,0)is a critical point for the function .What kind of critical point is it?
A)local minimum
B)saddle point
C)local maximum
D)none of these
A)local minimum
B)saddle point
C)local maximum
D)none of these

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
68
Let 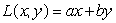 .Find values of a and b so that
.Find values of a and b so that 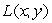 takes a maximum value of 4 on the unit circle
takes a maximum value of 4 on the unit circle 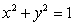 at the point
at the point 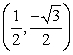 .
.
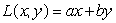 .Find values of a and b so that
.Find values of a and b so that 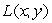 takes a maximum value of 4 on the unit circle
takes a maximum value of 4 on the unit circle 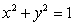 at the point
at the point 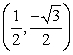 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
69
Let in the square S bounded by .Then is a critical point.What kind of critical point is it?
A)local maximum
B)local minimum
C)saddle point
D)none of these
A)local maximum
B)local minimum
C)saddle point
D)none of these

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
70
Let where k 0.Find the critical points of f.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
71
Let where k 0.Determine the values of k (if any)for which the critical point at (-1, 0)is a local minimum.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
72
Find three numbers x, y, and z, such that 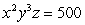 and
and 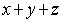 is minimal.What is this minimal sum?
is minimal.What is this minimal sum?
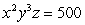 and
and 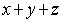 is minimal.What is this minimal sum?
is minimal.What is this minimal sum?
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
73
It can be shown that are the critical points of the function .Which of the following are classified correctly? Select all that apply.
A)(0,0)is a local minimum.
B)(1,0)is a local maximum.
C)(-1,0)is a local maximum.
D) is a saddle point.
E) is a local minimum.
A)(0,0)is a local minimum.
B)(1,0)is a local maximum.
C)(-1,0)is a local maximum.
D) is a saddle point.
E) is a local minimum.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
74
The level curves of f(x, y)are shown in the picture below. 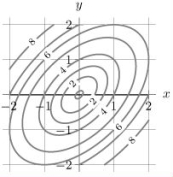 (a)Estimate the global maximum and minimum of f on the closed triangular region D with vertices at (-1, -1), (2, -1)and (-1, 2).
(a)Estimate the global maximum and minimum of f on the closed triangular region D with vertices at (-1, -1), (2, -1)and (-1, 2).
(b)Find the critical point(s)of f in the interior of the region D.
(c)Find the critical point(s)of f along the boundary of D.
 (a)Estimate the global maximum and minimum of f on the closed triangular region D with vertices at (-1, -1), (2, -1)and (-1, 2).
(a)Estimate the global maximum and minimum of f on the closed triangular region D with vertices at (-1, -1), (2, -1)and (-1, 2).(b)Find the critical point(s)of f in the interior of the region D.
(c)Find the critical point(s)of f along the boundary of D.

Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
75
Find the maximum and minimum values of 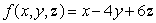 subject to the constraint
subject to the constraint 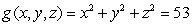 .
.
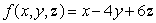 subject to the constraint
subject to the constraint 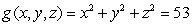 .
.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
76
The temperature at each point in the first quadrant is given by 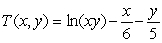 .Find the hottest point in the first quadrant and determine its temperature.
.Find the hottest point in the first quadrant and determine its temperature.
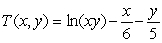 .Find the hottest point in the first quadrant and determine its temperature.
.Find the hottest point in the first quadrant and determine its temperature.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck
77
Find the maximum and minimum values of 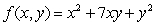 subject to the constraint
subject to the constraint 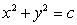 , with
, with 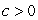 .Your answers may depend on c.
.Your answers may depend on c.
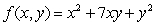 subject to the constraint
subject to the constraint 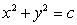 , with
, with 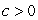 .Your answers may depend on c.
.Your answers may depend on c.
Unlock Deck
Unlock for access to all 77 flashcards in this deck.
Unlock Deck
k this deck


