Exam 15: Optimization- Local and Global Extrema
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Find the critical point of Do this by setting and optimizing subject to the constraint What are the global maximum and minimum values of f? Give your answer to 4 decimal places.
Free
(Essay)
4.8/5  (28)
(28)
Correct Answer:
Given that the quadratic Taylor polynomial of f at (4, 5)is decide whether is a critical point.If so, identify what sort of critical point it is.
Free
(Essay)
4.9/5  (40)
(40)
Correct Answer:
The point is not a critical point..
Consider the function Determine all local maxima, minima and saddle points of f.
Does f have a global maximum?
Free
(Essay)
4.8/5  (38)
(38)
Correct Answer:
(0,0)is a local maximum and a global maximum.
Suppose that Find and classify the critical point(s)as local maxima, local minima, or saddle points.
(Short Answer)
4.9/5  (45)
(45)
Let , where a, b are any positive numbers with a 4.
Find the minimum value of a such that the critical point will be a saddle point.
(Short Answer)
4.9/5  (40)
(40)
The level curves of f(x, y)are shown in the picture below. 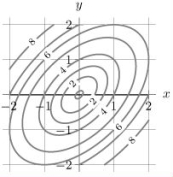 (a)Estimate the global maximum and minimum of f on the closed triangular region D with vertices at (-1, -1), (2, -1)and (-1, 2).
(b)Find the critical point(s)of f in the interior of the region D.
(c)Find the critical point(s)of f along the boundary of D.
(a)Estimate the global maximum and minimum of f on the closed triangular region D with vertices at (-1, -1), (2, -1)and (-1, 2).
(b)Find the critical point(s)of f in the interior of the region D.
(c)Find the critical point(s)of f along the boundary of D.
(Essay)
4.8/5  (29)
(29)
Find the maximum and minimum values of subject to the constraint , with .Your answers may depend on c.
(Essay)
4.9/5  (40)
(40)
A company has $250,000 to spend on labor and raw materials.Let L be the quantity of labor and R be the quantity of raw materials.The production output P of the company is cRL (here c is a positive constant).Suppose that each unit of labor costs $6000 and the unit price of raw materials is $2000.
Find the ratio of R to L that maximizes P.
(Short Answer)
4.9/5  (32)
(32)
Suppose that you want to find the maximum and minimum values of subject to the constraint x + 4y = 3.
Use the method of Lagrange multipliers to find the exact location(s)of any extrema.
(Essay)
4.8/5  (28)
(28)
Find all the critical points of and classify each as maximum, minimum, or saddle point. Select all possible choices.
(Multiple Choice)
4.8/5  (40)
(40)
Let .The constraint g(x, y)= 3 is sketched in the picture below.
In the picture, locate the point where f will have a global maximum subject to the constraint g(x, y)= 3. 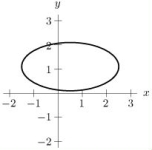
(Essay)
4.9/5  (39)
(39)
Use Lagrange multipliers to find the minimum value of 4xy on the circle .
(Essay)
4.8/5  (38)
(38)
The point (0,0)is a critical point for the function .What kind of critical point is it?
(Multiple Choice)
4.8/5  (34)
(34)
(a)Let .Find the maximum and minimum values of f on the curve
(b)Use the results of part (a)to find the maximum and minimum values of on the curve Explain your work.
(Essay)
4.9/5  (46)
(46)
The contour diagram of f is shown below. 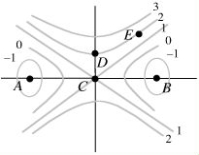 Find and classify the critical points.
Describe possible gradient vectors of f at points C, D and E.
Find and classify the critical points.
Describe possible gradient vectors of f at points C, D and E.
(Essay)
4.9/5  (38)
(38)
Consider the diagram shown below, which shows gradient vectors of a function f(x, y). 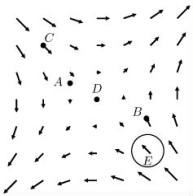 Which is less: f(A)or f(C)?
Which is less: f(A)or f(C)?
(Short Answer)
5.0/5  (37)
(37)
Find three numbers x, y, and z, such that and is minimal.What is this minimal sum?
(Essay)
4.9/5  (30)
(30)
Suppose there are two electric generators that burn natural gas and whose efficiency declines with output.The energy output is an increasing (but concave down)function of fuel input.Specifically, say
Output of generator 1 is
(Essay)
4.8/5  (36)
(36)
The function where a and b are constants is sometimes referred to as a "bump function" and is used to construct functions which take on maximum values at certain points.Show that f(x, y)has a maximum at (a, b).
(Essay)
4.8/5  (34)
(34)
Showing 1 - 20 of 77
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)