Deck 11: Differential Equations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/135
Play
Full screen (f)
Deck 11: Differential Equations
1
Which of the following functions are solutions to the differential equation ? (Mark all correct answers.)
A)
B)
C)
D)
A)
B)
C)
D)
2
Select the value(s)of w for which satisfies .
A)7
B)-7
C)49
D)-49
E)0
A)7
B)-7
C)49
D)-49
E)0
7
-7
-7
3
One of the solutions to the differential equation is a straight line.Take a point not on the line.Can a solution curve through cross the line?
False
4
Suppose and .Estimate and using the slope given by the differential equation.
A)4 and 3.9
B)5.95 and 17.75
C)3.95 and 3.9
D)7.95 and 17.95
E)2.2 and 2.4175
A)4 and 3.9
B)5.95 and 17.75
C)3.95 and 3.9
D)7.95 and 17.95
E)2.2 and 2.4175

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
5
For what value(s)of n (if any)is a solution to the differential equation ?
A)2
B)-2
C)4
D)-4
E)0
A)2
B)-2
C)4
D)-4
E)0

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
6
Mark all the true statements about the differential equation:
A)It is a first order differential equation.
B)It is a second order differential equation.
C)Any solutions to the differential equation would be of the form x = a.
D)Any solutions to the differential equation would be of the form y = f(x).
A)It is a first order differential equation.
B)It is a second order differential equation.
C)Any solutions to the differential equation would be of the form x = a.
D)Any solutions to the differential equation would be of the form y = f(x).

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
7
Which of the following functions are solutions to the differential equation ? (Mark all correct answers.)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
8
Suppose and .What is the best approximation of .
A)0.8
B)3.6
C)4.8
D)16
A)0.8
B)3.6
C)4.8
D)16

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
9
Suppose that the function P(t)satisfies the differential equation with the initial condition P(0)= 1.Consider the behavior of the graph of near a point , where (if such a point exists).Is the following graph consistent with P(t)? 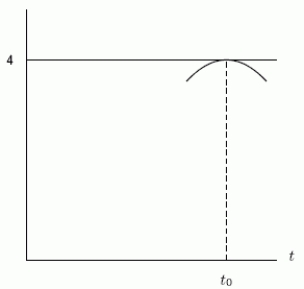


Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
10
Suppose that the function P(t)satisfies the differential equation with the initial condition P(0)= 1.Find P"(0).

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose that the function P(t)satisfies the differential equation 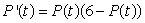 with the initial condition P(0)= 4.Which of the following is a possible graph for P(t)for small t > 0?
with the initial condition P(0)= 4.Which of the following is a possible graph for P(t)for small t > 0? 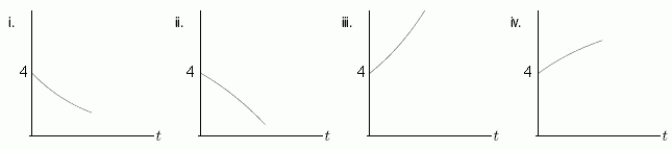
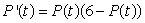 with the initial condition P(0)= 4.Which of the following is a possible graph for P(t)for small t > 0?
with the initial condition P(0)= 4.Which of the following is a possible graph for P(t)for small t > 0? 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
12
Given , find S if the initial velocity is 10 m/sec upward and the initial position is 5 m above the ground.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
13
Does satisfy ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
14
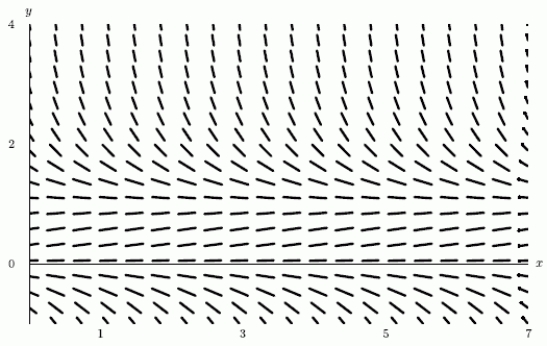
Which of the following equations corresponds with the slope field shown below?
I.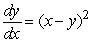 II.
II. 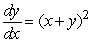 III.
III. 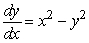 IV.None of them
IV.None of them 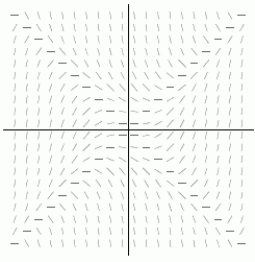
I.
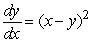 II.
II. 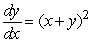 III.
III. 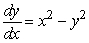 IV.None of them
IV.None of them 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
15
Which of the following equations corresponds with the slope field shown below?
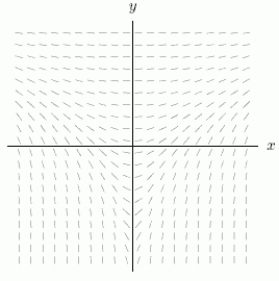
A)
B)
C)
D)
E)
F) None of them

A)
B)
C)
D)
E)
F) None of them

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
16
Is a solution to ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
17
Which of the following equations goes with is on the graph of each of the equations).
A)
B)
C)

A)
B)
C)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
18
Which of the following functions are solutions to the differential equation ? (Mark all correct answers)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
19
The slope field for the differential equation is shown below.Consider the solution curve to the differential equation starting at x = 0, y = 5, and ending at x = 5 and approximate the value of y when x is 5. 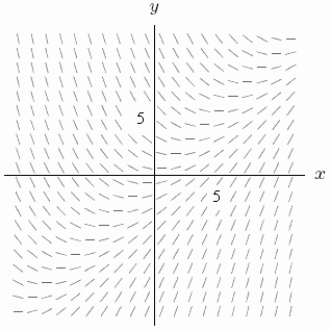
A)1.25
B)2.5
C)3.75
D)5

A)1.25
B)2.5
C)3.75
D)5

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
20
Which of the following functions are solutions to the differential equation ? (Mark all correct answers)
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
21
Consider the solution with y(0)= 0 to the differential equation 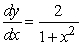 .Use Euler's method with 2 steps to approximate the value of
.Use Euler's method with 2 steps to approximate the value of 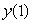 .Give your answer to 1 decimal place.
.Give your answer to 1 decimal place.
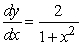 .Use Euler's method with 2 steps to approximate the value of
.Use Euler's method with 2 steps to approximate the value of 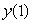 .Give your answer to 1 decimal place.
.Give your answer to 1 decimal place.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
22
Consider the differential equation 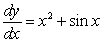 Solve the differential equation analytically given that
Solve the differential equation analytically given that 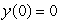 .Then approximate
.Then approximate 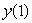 using Euler's method with three steps.Write a few sentences describing the error in Euler's method in this case, and what could be done to decrease the error.
using Euler's method with three steps.Write a few sentences describing the error in Euler's method in this case, and what could be done to decrease the error.
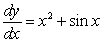 Solve the differential equation analytically given that
Solve the differential equation analytically given that 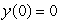 .Then approximate
.Then approximate 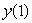 using Euler's method with three steps.Write a few sentences describing the error in Euler's method in this case, and what could be done to decrease the error.
using Euler's method with three steps.Write a few sentences describing the error in Euler's method in this case, and what could be done to decrease the error.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
23
Consider the solution with y(0)= 0 to the differential equation .If you use Euler's method with 1 million steps to approximate the exact value of , will your approximation be an over- or underestimate?
A)An overestimate
B)An underestimate
A)An overestimate
B)An underestimate

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
24
If a slope field for has constant slopes where y is constant, what do you know about ?
A) depends on y only.
B) depends on x only.
C) must be linear in y.
D) must be linear in x.
A) depends on y only.
B) depends on x only.
C) must be linear in y.
D) must be linear in x.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
25
The slope field for the differential equation 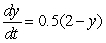 is shown below.Use Euler's method with N = 3 subdivisions of the interval
is shown below.Use Euler's method with N = 3 subdivisions of the interval  to approximate the value of y when t = 1, if you start at y = 1 and t = 0.Round your answer to 2 decimal places.
to approximate the value of y when t = 1, if you start at y = 1 and t = 0.Round your answer to 2 decimal places. 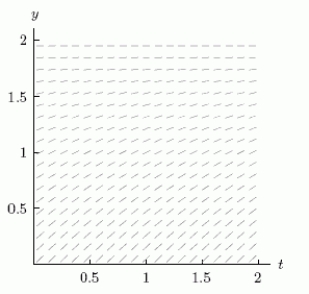
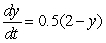 is shown below.Use Euler's method with N = 3 subdivisions of the interval
is shown below.Use Euler's method with N = 3 subdivisions of the interval 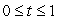 to approximate the value of y when t = 1, if you start at y = 1 and t = 0.Round your answer to 2 decimal places.
to approximate the value of y when t = 1, if you start at y = 1 and t = 0.Round your answer to 2 decimal places. 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
26
Consider the differential equation 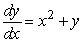 .Use Euler's method with two subdivisions to approximate the value of y when x = 2 on the solution curve that passes through (1,4).
.Use Euler's method with two subdivisions to approximate the value of y when x = 2 on the solution curve that passes through (1,4).
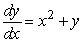 .Use Euler's method with two subdivisions to approximate the value of y when x = 2 on the solution curve that passes through (1,4).
.Use Euler's method with two subdivisions to approximate the value of y when x = 2 on the solution curve that passes through (1,4).
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
27
Consider the solution with y(0)= 0 to the differential equation 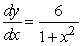 .Compute the exact value of y(1)and then round to 4 decimal places.
.Compute the exact value of y(1)and then round to 4 decimal places.
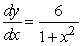 .Compute the exact value of y(1)and then round to 4 decimal places.
.Compute the exact value of y(1)and then round to 4 decimal places.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
28
The slope field for the differential equation is shown below.Use the slope field to estimate the solution starting from y = 3, x = 0, and use it to estimate the value of y when x = 1. 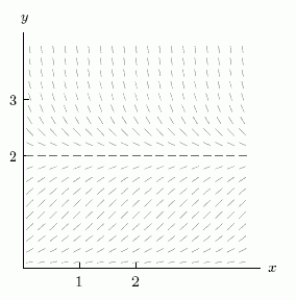
A)1.2
B)1.5
C)1.8
D)2.1

A)1.2
B)1.5
C)1.8
D)2.1

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
29
Is the equation 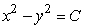 , for C a constant, a solution to the differential equation
, for C a constant, a solution to the differential equation 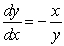 ?
?
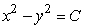 , for C a constant, a solution to the differential equation
, for C a constant, a solution to the differential equation 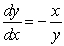 ?
?
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
30
The slope field for the differential equation 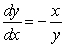 is shown below.Starting from the point
is shown below.Starting from the point 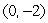 , use Euler's method with N = 3 subdivisions to approximate the value of y when x = 1.Round to 2 decimal places.
, use Euler's method with N = 3 subdivisions to approximate the value of y when x = 1.Round to 2 decimal places. 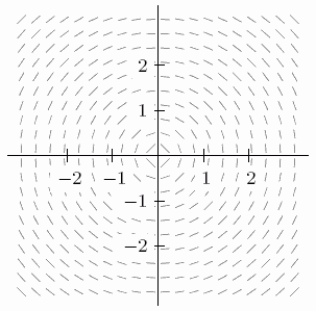
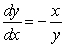 is shown below.Starting from the point
is shown below.Starting from the point 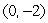 , use Euler's method with N = 3 subdivisions to approximate the value of y when x = 1.Round to 2 decimal places.
, use Euler's method with N = 3 subdivisions to approximate the value of y when x = 1.Round to 2 decimal places. 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
31
Solve the differential equation subject to .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
32
The slope field for the differential equation 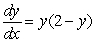 is shown below.Use the Euler's method with N = 4 subdivisions of the interval
is shown below.Use the Euler's method with N = 4 subdivisions of the interval 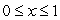 to approximate the value of y when x = 1, if you start at y = 1 and x = 0.Round your answer to 2 decimal places.
to approximate the value of y when x = 1, if you start at y = 1 and x = 0.Round your answer to 2 decimal places. 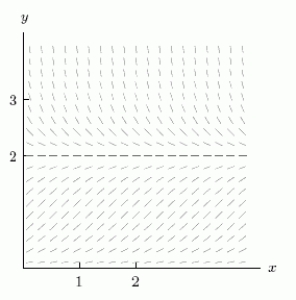
 is shown below.Use the Euler's method with N = 4 subdivisions of the interval
is shown below.Use the Euler's method with N = 4 subdivisions of the interval 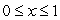 to approximate the value of y when x = 1, if you start at y = 1 and x = 0.Round your answer to 2 decimal places.
to approximate the value of y when x = 1, if you start at y = 1 and x = 0.Round your answer to 2 decimal places. 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
33
On the slope field for the differential equation 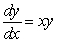 , sketch the solution curve in the fourth quadrant that goes through the point (0, -1).
, sketch the solution curve in the fourth quadrant that goes through the point (0, -1). 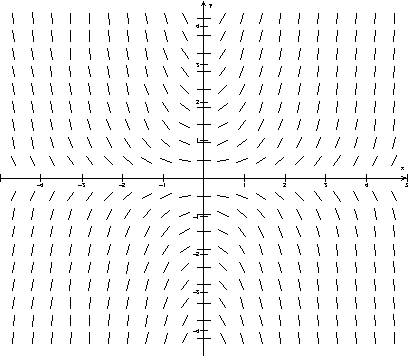
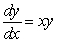 , sketch the solution curve in the fourth quadrant that goes through the point (0, -1).
, sketch the solution curve in the fourth quadrant that goes through the point (0, -1). 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
34
Use Euler's method with five steps to approximate a solution to the differential equation 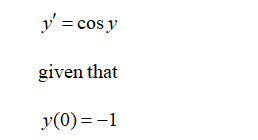
. Give both a numerical solution by filling in the table of values, and a graphical solution by plotting your points.
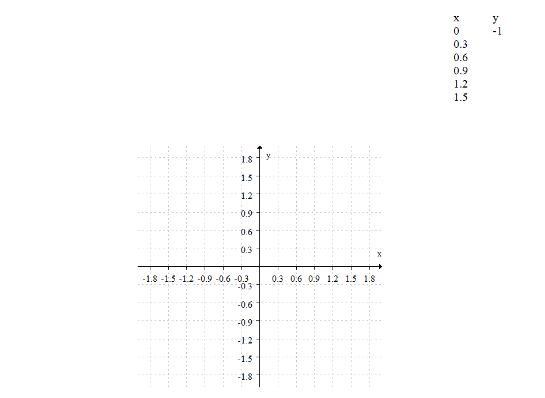
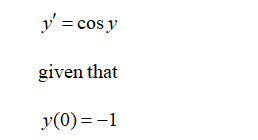
. Give both a numerical solution by filling in the table of values, and a graphical solution by plotting your points.


Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
35
Sketch a slope field for the differential equation 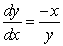 using the points indicated on the axes.
using the points indicated on the axes. 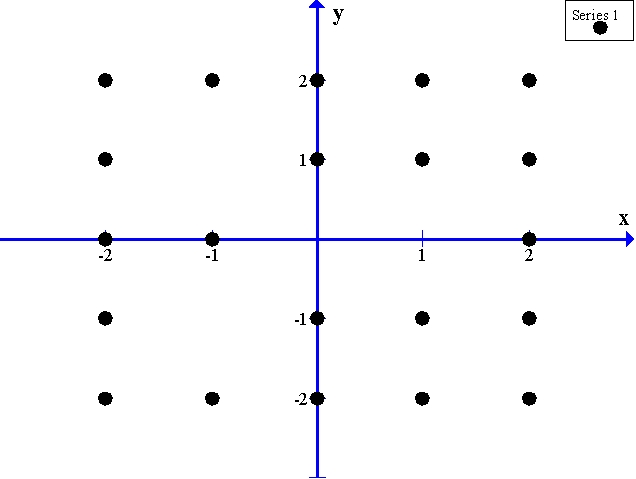
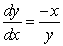 using the points indicated on the axes.
using the points indicated on the axes. 

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
36
If all the solution curves for have as a horizontal asymptote, does it follow that either or ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
37
The slope field for the differential equation is shown below.If you start from the point and use Euler's method with N = 3 subdivisions to approximate the value of y when x = 1, is your answer an underestimate or overestimate? 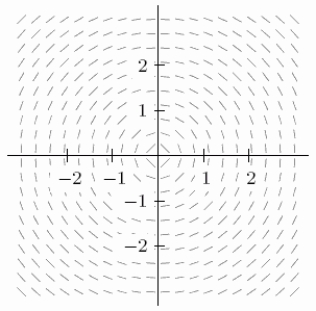
A)An overestimate
B)An underestimate

A)An overestimate
B)An underestimate

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
38
The slope field for the differential equation is shown below.Consider the solution starting from y = 0.5, t = 0, and use it to estimate the value of y when t = 1. 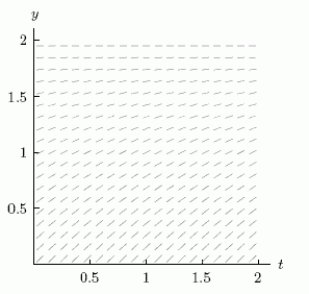
A)0.5
B)0.8
C)1.1
D)1.4

A)0.5
B)0.8
C)1.1
D)1.4

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
39
Consider the differential equation .If you use Euler's method to approximate the value of y when x = 2 on the solution curve that passes through (1,4), is your approximation an underestimate or overestimate?
A)An underestimate
B)An overestimate
A)An underestimate
B)An overestimate

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
40
For any constant C, is a solution to the differential equation .Find the solution through the point (0, -4).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
41
Solve if y = 0 when x = 2.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
42
Find the solution to the differential equation satisfying .Select all that apply.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
43
Is a solution to the differential equation (for some constant C)?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
44
Find the solution to the differential equation with , for all x.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
45
Solve the differential equation 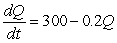 subject to
subject to 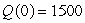 and sketch your solution.There is a horizontal asymptote at Q = _____.
and sketch your solution.There is a horizontal asymptote at Q = _____.
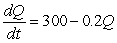 subject to
subject to 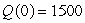 and sketch your solution.There is a horizontal asymptote at Q = _____.
and sketch your solution.There is a horizontal asymptote at Q = _____.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
46
Solve , with N(0)= 0 and sketch the solution for t 0.There is a horizontal asymptote at N = _____.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
47
Find the solution to the differential equation satisfying .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
48
Is the slope field for the differential equation symmetric about the y-axis?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
49
Solve , with N(0)= 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
50
Find the solution to the differential equation if when x = 1.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
51
Is a solution to the differential equation (for some constant C)?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
52
Is the solution to the differential equation with ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
53
Find the solution to the differential equation passing through .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
54
Find the solution to the differential equation with .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
55
Is the general solution to the differential equation ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
56
Solve if y = 1 when t = 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
57
Solve if when .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
58
What is the minimum value of the solution to the differential equation with ?
A)6
B)0
C) /e
D) e
A)6
B)0
C) /e
D) e

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
59
Solve if y = 4 when x = 0.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
60
Is the general solution to the differential equation ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
61
Cesium 137 (Cs137)is a short-lived radioactive isotope.It decays at a rate proportional to the amount of itself present and has a half-life of 30 years (i.e., the amount of Cs137 remaining t years after A0 mg of the radioactive isotope is released is given by 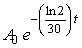 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.1 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.In the long run, approximately how many mg of Cs137 will there be? Round to 2 decimal places.
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.1 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.In the long run, approximately how many mg of Cs137 will there be? Round to 2 decimal places.
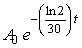 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.1 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.In the long run, approximately how many mg of Cs137 will there be? Round to 2 decimal places.
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.1 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.In the long run, approximately how many mg of Cs137 will there be? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
62
The population of aphids on a rose plant increases at a rate proportional to the number present.In 3 days the population grew from 700 to 1400.How many aphids were there on the day before there were 700 aphids? Round to the nearest whole number.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
63
Consider the Hakosalo residence in Oulu, Finland.Assume that heat is lost from the house only through windows and the rate of change of temperature in °F/hr is proportional to the difference in temperature between the outside and the inside.The constant of proportionality is 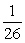 .Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.At 5 pm the heat is turned on.The heater generates an amount of energy that would raise the inside temperature by 2°F per hour if there were no heat loss.If the heat is left on indefinitely, what temperature will the inside of the house approach? Do not include units in your answer.
.Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.At 5 pm the heat is turned on.The heater generates an amount of energy that would raise the inside temperature by 2°F per hour if there were no heat loss.If the heat is left on indefinitely, what temperature will the inside of the house approach? Do not include units in your answer.
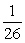 .Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.At 5 pm the heat is turned on.The heater generates an amount of energy that would raise the inside temperature by 2°F per hour if there were no heat loss.If the heat is left on indefinitely, what temperature will the inside of the house approach? Do not include units in your answer.
.Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.At 5 pm the heat is turned on.The heater generates an amount of energy that would raise the inside temperature by 2°F per hour if there were no heat loss.If the heat is left on indefinitely, what temperature will the inside of the house approach? Do not include units in your answer.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
64
The population of aphids on a rose plant increases at a rate proportional to the number present.In 3 days the population grew from 600 to 1400.How many days does it take for the population to get 10 times as large? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
65
Is the general solution to the differential equation ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
66
Suppose there is a new kind of savings certificate that starts out paying 2% annual interest and increases the interest rate by 1% each additional year that the money is left on deposit.(Assume that interest is compounded continuously and that the interest rate increases continuously.)Write a differential equation that gives the rate of change in the balance B(t)at time t, and solve it assuming an initial deposit of $500.What is your equation?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
67
A bank account earns interest at a rate of 5% per year, compounded continuously.Money is deposited into the account in a continuous cash flow at a rate of $1000 per year.Use differential equations to find the amount of money in the bank account after 10 years, assuming an initial balance of $3000.Round to the nearest cent.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
68
Cesium 137 (Cs137)is a short-lived radioactive isotope.It decays at a rate proportional to the amount of itself present and has a half-life of 30 years (i.e., the amount of Cs137 remaining t years after A0 mg of the radioactive isotope is released is given by 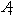 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following differential equations have a solution R(t), the amount (in mg)of Cs137 in t years? (We are assuming R(0)= 0.)
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following differential equations have a solution R(t), the amount (in mg)of Cs137 in t years? (We are assuming R(0)= 0.)
A)
B)
C)
D)
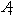 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following differential equations have a solution R(t), the amount (in mg)of Cs137 in t years? (We are assuming R(0)= 0.)
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following differential equations have a solution R(t), the amount (in mg)of Cs137 in t years? (We are assuming R(0)= 0.)A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
69
Newton's Law of Cooling states that the rate of change of temperature of an object is proportional to the difference between the temperature of the object and the temperature of the surrounding air.A detective discovers a corpse in an abandoned building, and finds its temperature to be 26°C.An hour later its temperature is 18°C.Assume that the air temperature is 6°C, that normal body temperature is 37°C, and that Newton's Law of Cooling applies to the corpse.How many hours has the corpse been dead at the moment it is discovered? Round to 2 decimal places.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
70
Cesium 137 (Cs137)is a short-lived radioactive isotope.It decays at a rate proportional to the amount of itself present and has a half-life of 30 years (i.e., the amount of Cs137 remaining t years after A0 mg of the radioactive isotope is released is given by 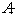 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following integrals give the total amount of Cs137 T years after the plant began operations?
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following integrals give the total amount of Cs137 T years after the plant began operations?
A)
B)
C)
D)
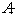 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following integrals give the total amount of Cs137 T years after the plant began operations?
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.12 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Which of the following integrals give the total amount of Cs137 T years after the plant began operations?A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
71
Mark all of the differential equations that are NOT separable.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
72
The population of aphids on a rose plant increases at a rate proportional to the number present.In 5 days the population grew from 700 to 1100.Which of the following formulas give for the population of aphids at time t in days, where t = 0 is the day when there were 700 aphids?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
73
Suppose there is a new kind of savings certificate that starts out paying 3.5% annual interest and increases the interest rate by 1% each additional year that the money is left on deposit.(Assume that interest is compounded continuously and that the interest rate increases continuously.)Assuming an initial deposit of $1500, which of the following investment choices is better?
A)Investing the money at a fixed interest rate of 5% for 4 years.
B)Investing the money in the new kind of savings certificate for 4 years.
A)Investing the money at a fixed interest rate of 5% for 4 years.
B)Investing the money in the new kind of savings certificate for 4 years.

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
74
Cesium 137 (Cs137)is a short-lived radioactive isotope.It decays at a rate proportional to the amount of itself present and has a half-life of 30 years (i.e., the amount of Cs137 remaining t years after A0 mg of the radioactive isotope is released is given by 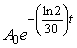 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.14 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Since Cs137 poses a great health risk, the government says that the maximum amount of Cs137 acceptable in the surrounding environment is 1 mg (spread over the surroundings).How many mg per year of the isotope can the station release and still be in compliance with the regulations? Round to 2 decimal places.
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.14 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Since Cs137 poses a great health risk, the government says that the maximum amount of Cs137 acceptable in the surrounding environment is 1 mg (spread over the surroundings).How many mg per year of the isotope can the station release and still be in compliance with the regulations? Round to 2 decimal places.
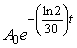 ).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.14 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Since Cs137 poses a great health risk, the government says that the maximum amount of Cs137 acceptable in the surrounding environment is 1 mg (spread over the surroundings).How many mg per year of the isotope can the station release and still be in compliance with the regulations? Round to 2 decimal places.
).As a result of its operations, a nuclear power plant releases Cs137 at a rate of 0.14 mg per year.The plant began its operations in 1990, which we will designate as t = 0.Assume there is no other source of this particular isotope.Since Cs137 poses a great health risk, the government says that the maximum amount of Cs137 acceptable in the surrounding environment is 1 mg (spread over the surroundings).How many mg per year of the isotope can the station release and still be in compliance with the regulations? Round to 2 decimal places.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
75
Is the general solution to the differential equation ?

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the Hakosalo residence in Oulu, Finland.Assume that heat is lost from the house only through windows and the rate of change of temperature in °F/hr is proportional to the difference in temperature between the outside and the inside.The constant of proportionality is 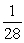 .Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.Use differential equations to find the temperature in the house at 5 pm.Round to one decimal place, and do not include units in your answer.
.Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.Use differential equations to find the temperature in the house at 5 pm.Round to one decimal place, and do not include units in your answer.
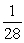 .Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.Use differential equations to find the temperature in the house at 5 pm.Round to one decimal place, and do not include units in your answer.
.Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.Use differential equations to find the temperature in the house at 5 pm.Round to one decimal place, and do not include units in your answer.
Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
77
Suppose there is a new kind of savings certificate that starts out paying 1.5% annual interest and increases the interest rate by 1% each additional year that the money is left on deposit.(Assume that interest is compounded continuously and that the interest rate increases continuously.)Which of the following differential equations gives the rate of change in the balance B(t)at time t?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
78
Consider the Hakosalo residence in Oulu, Finland.Assume that heat is lost from the house only through windows and the rate of change of temperature in °F/hr is proportional to the difference in temperature between the outside and the inside.The constant of proportionality is .Assume that it is 10°F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.Which of the following differential equations reflects the rate of change of the temperature in the house between noon and 5 pm?
A) ,
B) ,
C) ,
D) ,
A) ,
B) ,
C) ,
D) ,

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
79
Solve the differential equation using separation of variables.
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck
80
Consider the Hakosalo residence in Oulu, Finland.Assume that heat is lost from the house only through windows and the rate of change of temperature in °F/hr is proportional to the difference in temperature between the outside and the inside.The constant of proportionality is .Assume that it is 10° F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.At 5 pm the heat is turned on.The heater generates an amount of energy that would raise the inside temperature by 2°F per hour if there were no heat loss.Which of the following differential equations reflect what happens to the inside temperature after the heat is turned on?
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 135 flashcards in this deck.
Unlock Deck
k this deck


