Exam 11: Differential Equations
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
Consider the Hakosalo residence in Oulu, Finland.Assume that heat is lost from the house only through windows and the rate of change of temperature in °F/hr is proportional to the difference in temperature between the outside and the inside.The constant of proportionality is .Assume that it is 10° F outside constantly.On a Thursday at noon the temperature inside the house was 65°F and the heat was turned off until 5 pm.At 5 pm the heat is turned on.The heater generates an amount of energy that would raise the inside temperature by 2°F per hour if there were no heat loss.Which of the following differential equations reflect what happens to the inside temperature after the heat is turned on?
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
D
Is the solution of passing through (0, 1)the same as the solution passing through (0, 0), except it has been shifted one unit upward?
Free
(True/False)
4.9/5  (37)
(37)
Correct Answer:
True
A spherical raindrop evaporates at a rate proportional to its surface area.If V = volume of the raindrop and S = surface area, which of the following is a differential equation for ?
Free
(Multiple Choice)
4.7/5  (29)
(29)
Correct Answer:
A
Suppose the equations , describe the rates of growth of two interacting species, where x is the number of species A, measured in thousands, and y is the number of species B, measured in thousands.The slope field in the xy-phase plane is shown below.Sketch the trajectory for initial conditions of x = 1.5, y = 0.5.(In other words, there are initially 1500 of species A and 500 of species B).Is species A increasing or decreasing?
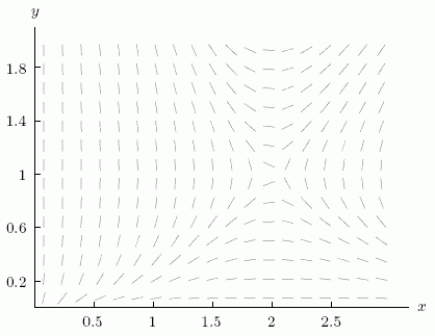
(Short Answer)
4.8/5  (28)
(28)
The rate of change of a population for a species is given by P 
 where P measures the population in thousands at time t months.The species starts with 1000 members (P = 1)at time t = 0.Assume that the differential equation holds indefinitely.If P = 0 is an equilibrium value of the population, is it stable or unstable? (If it is not an equilibrium value, enter "neither")
where P measures the population in thousands at time t months.The species starts with 1000 members (P = 1)at time t = 0.Assume that the differential equation holds indefinitely.If P = 0 is an equilibrium value of the population, is it stable or unstable? (If it is not an equilibrium value, enter "neither")
(Short Answer)
4.9/5  (36)
(36)
There is a theory that says the rate at which information spreads by word of mouth is proportional to the product of the number of people who have heard the information and the number who have not.Suppose the total population is N.Which of the following differential equations describe the rate, , at which the information spreads by word of mouth?
(Multiple Choice)
4.9/5  (30)
(30)
On the slope field for the differential equation , sketch the solution curve in the fourth quadrant that goes through the point (0, -1). 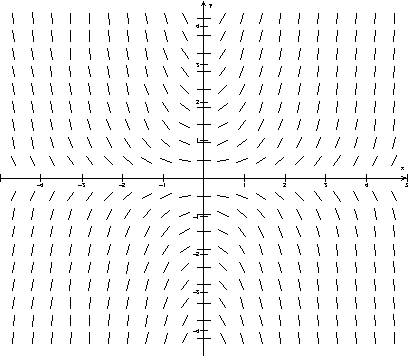
(Essay)
4.8/5  (39)
(39)
If a slope field for has constant slopes where y is constant, what do you know about ?
(Multiple Choice)
4.8/5  (32)
(32)
Find the solution to the differential equation given the boundary conditions and .
(Multiple Choice)
4.9/5  (34)
(34)
The population of aphids on a rose plant increases at a rate proportional to the number present.In 3 days the population grew from 600 to 1400.How many days does it take for the population to get 10 times as large? Round to 2 decimal places.
(Short Answer)
4.8/5  (32)
(32)
Verify that is a solution of .Suppose that y describes the motion of a mass on a spring. How does the motion start when t = 0?
(Multiple Choice)
4.9/5  (36)
(36)
Consider the solution with y(0)= 0 to the differential equation .Compute the exact value of y(1)and then round to 4 decimal places.
(Short Answer)
4.8/5  (36)
(36)
The rate of change of a population for a species is given by 
 where P measures the population in thousands at time t months.The species starts with 1000 members (P = 1)at time t = 0.Assume that the differential equation holds indefinitely.Which of the following is a graph of the population as a function of time?
where P measures the population in thousands at time t months.The species starts with 1000 members (P = 1)at time t = 0.Assume that the differential equation holds indefinitely.Which of the following is a graph of the population as a function of time? 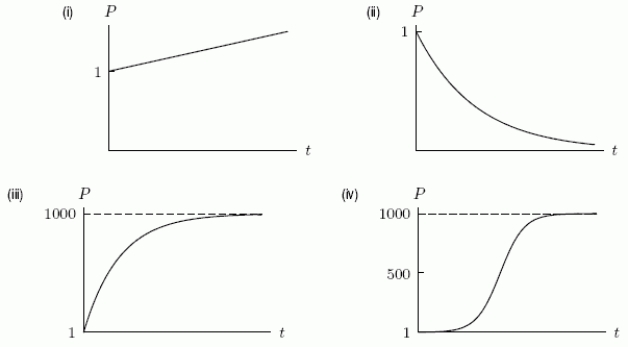
(Short Answer)
4.8/5  (37)
(37)
Let x be the number of reptiles, y be the number of mammals, and z be the number of plants on the island of Komodo, all measured in thousands (e.g., x = 50 means 50,000 reptiles).The following differential equations give the rates of growth of reptiles, mammals, and plants on the island: =-0.6x-0.12xy+0.0024xz =-0.1y+0.01xy =6z-0.006-0.1xz Who is eating whom on Komodo? Mark all that apply.
(Multiple Choice)
4.8/5  (40)
(40)
In an electrical circuit, a damping force can be provided by a resistor.In this case, the differential equation describes the charge Q on a capacitor in a circuit with inductance L, capacitance C, and resistance R.Suppose L = 1 henry, R = 50 ohms and C = 0.0016 farads.Find a formula for the charge, Q, when and .
(Essay)
4.7/5  (35)
(35)
Showing 1 - 20 of 135
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)