Deck 14: Differentiating Functions of Several Variables
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/129
Play
Full screen (f)
Deck 14: Differentiating Functions of Several Variables
1
Suppose 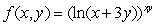 .
.
Use a difference quotient to estimate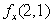 and
and 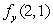 with h = 0.01.Give your answers to 3 decimal places.
with h = 0.01.Give your answers to 3 decimal places.
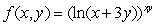 .
.Use a difference quotient to estimate
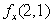 and
and 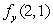 with h = 0.01.Give your answers to 3 decimal places.
with h = 0.01.Give your answers to 3 decimal places.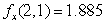 and
and 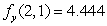 .
. 2
Find if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)
3
If everywhere, then f(x, y)is a constant.
False
4
Find .
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
5
There exists a function f(x, y)with fx = 2y and fy = 3x.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
6
The ideal gas law states that 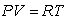 for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
Find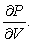
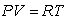 for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.Find
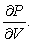

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
7
Estimate the value of 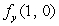 from the given contour diagram of f.
from the given contour diagram of f. 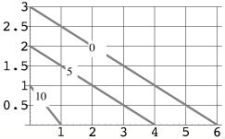
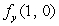 from the given contour diagram of f.
from the given contour diagram of f. 

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
8
The monthly mortgage payment in dollars, P, for a house is a function of three variables P = f(A, r, N), where A is the amount borrowed in dollars, r is the interest rate, and N is the number of years before the mortgage is paid off.It is given that: 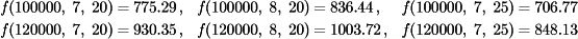 Estimate the value of
Estimate the value of 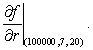
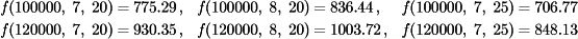 Estimate the value of
Estimate the value of 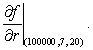

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
9
The figure below shows the graph of z = f(x, y)and its intersection with various planes.(The x and y-axes have the same scale.) What is the sign of ? 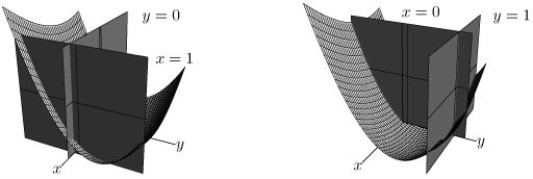
A)Negative
B)Positive

A)Negative
B)Positive

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
10
Find 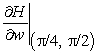 to 2 decimal places if
to 2 decimal places if 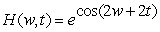 .
.
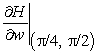 to 2 decimal places if
to 2 decimal places if 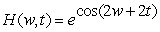 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
11
The level curves of a function z = f(x, y)are shown below.Assume that the scales along the x and y axes are the same. 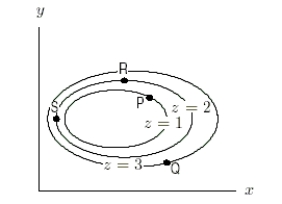


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
12
If $P is invested in a bank account earning r% interest a year, compounded continuously, the balance, $B, at the end of t years is given by 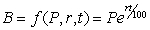 (a)What are the units of
(a)What are the units of 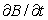 ?
?
(b)What is the practical interpretation (in terms of money)of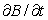 ?
?
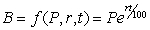 (a)What are the units of
(a)What are the units of 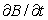 ?
?(b)What is the practical interpretation (in terms of money)of
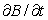 ?
?
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
13
The cross-sections of f when x is fixed at x = 1 and when y is fixed at y = 2 are given below.
Determine, if possible, the sign of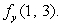
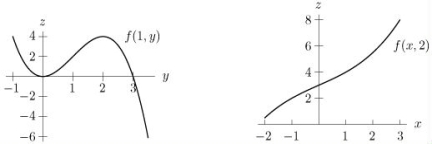
Determine, if possible, the sign of

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
14
Given the contour diagram shown below, state whether is positive, negative or nearly zero. 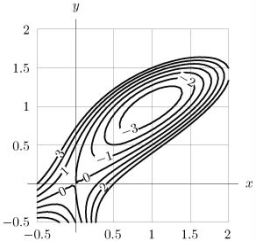
A)Almost zero
B)Negative
C)Positive
D)Undefined

A)Almost zero
B)Negative
C)Positive
D)Undefined

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
15
The ideal gas law states that 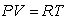 for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
A mole of a certain gas is at a temperature of 290° K, a pressure of 1 atmosphere, and a volume of 0.04 m3.
What is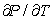 for this gas?
for this gas?
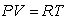 for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.A mole of a certain gas is at a temperature of 290° K, a pressure of 1 atmosphere, and a volume of 0.04 m3.
What is
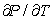 for this gas?
for this gas?
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
16
If $P is invested in a bank account earning r% interest a year, compounded continuously, the balance, $B, at the end of t years is given by 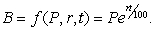 Find
Find 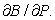
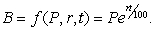 Find
Find 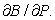

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
17
The consumption of beef, C (in pounds per week per household)is given by the function C = f(I, p), where I is the household income in thousands of dollars per year, and p is the price of beef in dollars per pound. Do you expect to be positive or negative?
A)Negative
B)Positive
A)Negative
B)Positive

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
18
The monthly mortgage payment in dollars, P, for a house is a function of three variables P = f(A, r, N), where A is the amount borrowed in dollars, r is the interest rate, and N is the number of years before the mortgage is paid off.It is given that: Estimate the value of and interpret your answer in terms of a mortgage payment.Select all answers that apply.
A)We are currently borrowing $100,000 at 7% interest rate on a 20-year mortgage.
B)The monthly payment will go up by approximately $0.007753 for each extra percentage point charged.
C)The monthly payment will go up by approximately $0.007753 for each extra dollar we borrow.
D)The monthly payment will go up by approximately $0.007753 for each extra year of the mortgage.
E)The monthly payment will go down by approximately $0.007753 for each extra dollar we borrow.
A)We are currently borrowing $100,000 at 7% interest rate on a 20-year mortgage.
B)The monthly payment will go up by approximately $0.007753 for each extra percentage point charged.
C)The monthly payment will go up by approximately $0.007753 for each extra dollar we borrow.
D)The monthly payment will go up by approximately $0.007753 for each extra year of the mortgage.
E)The monthly payment will go down by approximately $0.007753 for each extra dollar we borrow.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
19
Given the contour diagram shown below
(a)Sketch a graph of f(1, y).
(b)Sketch a graph of f(x, 0).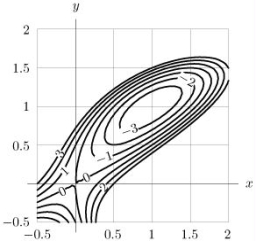
(a)Sketch a graph of f(1, y).
(b)Sketch a graph of f(x, 0).


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
20
Suppose that the price P (in dollars)to purchase a used car is a function of C, its original cost (in dollars), and its age A (in years).So P = f(C,A). What is the sign of
A)Positive
B)Negative
A)Positive
B)Negative

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
21
Use the differential of to find a linear approximation of f at the point (1, /4).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
22
Determine the tangent plane to 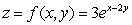 at (x, y)= (2, 1).
at (x, y)= (2, 1).
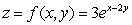 at (x, y)= (2, 1).
at (x, y)= (2, 1).
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
23
The equations of the tangent planes to the graph z = f(x, y)at the points (0, -2), (2, 1)are 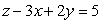 and
and 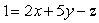 , respectively.Determine the value of
, respectively.Determine the value of 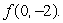 State whether the value you find is exact or an approximation.
State whether the value you find is exact or an approximation.
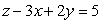 and
and 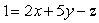 , respectively.Determine the value of
, respectively.Determine the value of 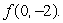 State whether the value you find is exact or an approximation.
State whether the value you find is exact or an approximation.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
24
The volume 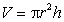 of a right circular cylinder is to be calculated from measured values of r and h.Suppose r is measured with an error of no more than 2.5% and h with an error of no more than 1%.Using differentials, estimate the percentage error in the calculation of V.
of a right circular cylinder is to be calculated from measured values of r and h.Suppose r is measured with an error of no more than 2.5% and h with an error of no more than 1%.Using differentials, estimate the percentage error in the calculation of V.
(In general, in measuring a quantity Q, the percentage error is dQ/Q.)
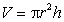 of a right circular cylinder is to be calculated from measured values of r and h.Suppose r is measured with an error of no more than 2.5% and h with an error of no more than 1%.Using differentials, estimate the percentage error in the calculation of V.
of a right circular cylinder is to be calculated from measured values of r and h.Suppose r is measured with an error of no more than 2.5% and h with an error of no more than 1%.Using differentials, estimate the percentage error in the calculation of V.(In general, in measuring a quantity Q, the percentage error is dQ/Q.)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
25
Let 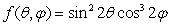 .Find
.Find 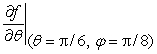 to 3 decimal places.
to 3 decimal places.
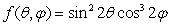 .Find
.Find 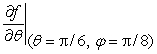 to 3 decimal places.
to 3 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
26
Let 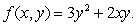 Use the appropriate partial derivative to find the slope of the cross-section at the given point.
Use the appropriate partial derivative to find the slope of the cross-section at the given point.
(a)The cross-section f(x, 2)at the point (3, 2).
(b)The cross-section f(1, y)at the point (1, -2).
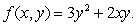 Use the appropriate partial derivative to find the slope of the cross-section at the given point.
Use the appropriate partial derivative to find the slope of the cross-section at the given point.(a)The cross-section f(x, 2)at the point (3, 2).
(b)The cross-section f(1, y)at the point (1, -2).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
27
If is a unit vector and the level curves of f(x, y)are given below, then at point P we have 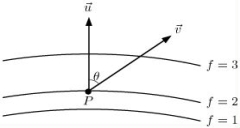


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
28
Estimate 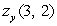 numerically if
numerically if 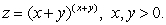
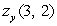 numerically if
numerically if 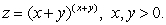

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
29
For the function find a unit vector in the direction of the steepest increase at the point (a, b)= (1, 1).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
30
Let 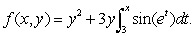 Find
Find 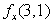 and
and 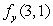 to four decimal places.
to four decimal places.
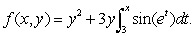 Find
Find 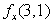 and
and 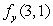 to four decimal places.
to four decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
31
Find an equation for the tangent plane to the graph of 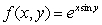 at
at 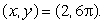
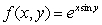 at
at 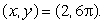

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
32
The depth of a pond at the point with coordinates (x, y)is given by 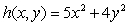 .(Assume that x, y, and h are measured in feet.)If a boat at the point (-3, -5)is sailing in the direction of the vector
.(Assume that x, y, and h are measured in feet.)If a boat at the point (-3, -5)is sailing in the direction of the vector 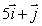 ,
,
then at what rate is the depth changing?
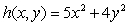 .(Assume that x, y, and h are measured in feet.)If a boat at the point (-3, -5)is sailing in the direction of the vector
.(Assume that x, y, and h are measured in feet.)If a boat at the point (-3, -5)is sailing in the direction of the vector 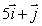 ,
,then at what rate is the depth changing?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
33
Find the gradient of the function 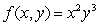 at the point
at the point 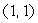 and use the result to obtain a linear approximation for
and use the result to obtain a linear approximation for 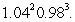
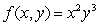 at the point
at the point 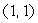 and use the result to obtain a linear approximation for
and use the result to obtain a linear approximation for 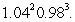

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
34
Find z/ x if

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
35
Find the differential of the function 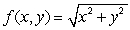 at the point (3, 4).
at the point (3, 4).
A point is measured to be 3 units from the y-axis with an error of ±0.01 and 4 units from the x-axis with an error of ±0.02.Approximate the error in computing its distance from the origin.
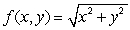 at the point (3, 4).
at the point (3, 4).A point is measured to be 3 units from the y-axis with an error of ±0.01 and 4 units from the x-axis with an error of ±0.02.Approximate the error in computing its distance from the origin.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
36
The table of some values of f(x, y)is given below.Find a local linearization of f at (1 , 2). 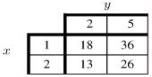


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
37
If is a unit vector and the level curves of f(x, y)are given below, then at point P we have 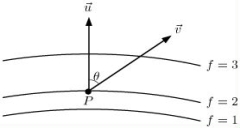


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
38
If a function z = g(x, y)has g(1, 2)= -5, gx(1, 2)= 4 and gy(1, 2)= 3, find the equation of the plane tangent to the surface z = g(x, y)at the point where x = 1 and y = 2.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
39
Calculate the following derivative: 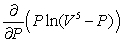 .
.
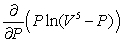 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose that Find an equation for the tangent plane to f at the point (3, 0).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
41
Let Find the gradient vector of f at the point (-1, 2).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
42
Find the equation of the tangent plane to at the point (-4, 1, 3).
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
43
An ant is walking along the surface which is the graph of the function 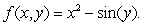 (a)When the ant is at the point (1, 0, 1), what direction should it move in order to be moving on the surface in the direction of greatest ascent?
(a)When the ant is at the point (1, 0, 1), what direction should it move in order to be moving on the surface in the direction of greatest ascent?
(b)If the ant moves in this direction at a speed of 6 units per second, what is the rate of change of height of the ant?
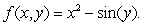 (a)When the ant is at the point (1, 0, 1), what direction should it move in order to be moving on the surface in the direction of greatest ascent?
(a)When the ant is at the point (1, 0, 1), what direction should it move in order to be moving on the surface in the direction of greatest ascent?(b)If the ant moves in this direction at a speed of 6 units per second, what is the rate of change of height of the ant?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
44
Given that f(2, 4)= 1.5 and f(2.1, 4.4)= 2.1, estimate the value of 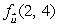 , where
, where 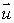 is the unit vector in the direction of
is the unit vector in the direction of 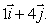 Give your answer to four decimal places.
Give your answer to four decimal places.
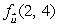 , where
, where 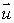 is the unit vector in the direction of
is the unit vector in the direction of 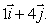 Give your answer to four decimal places.
Give your answer to four decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
45
Suppose || f(a, b, c)||=19.Is it possible to choose a direction from (a, b, c)so that in that direction is -19?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
46
Let 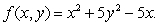 What is the direction of maximum rate of change of f at (1, 1)?
What is the direction of maximum rate of change of f at (1, 1)?
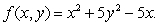 What is the direction of maximum rate of change of f at (1, 1)?
What is the direction of maximum rate of change of f at (1, 1)?
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
47
Suppose that as you move away from the point (2, 0, 2), the function increases most rapidly in the direction 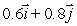 and the rate of increase of f in this direction is 7.At what rate is f increasing as you move away from (2, 0, 2)in the direction of
and the rate of increase of f in this direction is 7.At what rate is f increasing as you move away from (2, 0, 2)in the direction of 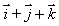 ? Give your answer to 4 decimal places.
? Give your answer to 4 decimal places.
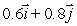 and the rate of increase of f in this direction is 7.At what rate is f increasing as you move away from (2, 0, 2)in the direction of
and the rate of increase of f in this direction is 7.At what rate is f increasing as you move away from (2, 0, 2)in the direction of 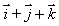 ? Give your answer to 4 decimal places.
? Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
48
If , then .

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
49
Consider the function 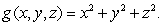 (a)Describe the level set g = 16.
(a)Describe the level set g = 16.
(b)Find a vector perpendicular to the tangent plane to the level set g = 16 at the point (-1, 2, 2).
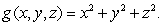 (a)Describe the level set g = 16.
(a)Describe the level set g = 16.(b)Find a vector perpendicular to the tangent plane to the level set g = 16 at the point (-1, 2, 2).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
50
Let 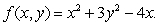 What is the maximum rate of change of f at (2, 1)?
What is the maximum rate of change of f at (2, 1)?
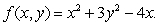 What is the maximum rate of change of f at (2, 1)?
What is the maximum rate of change of f at (2, 1)?
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose f(x, y)is a function of x and y and define 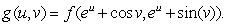 Find
Find 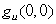 given that
given that 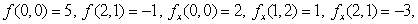 and
and 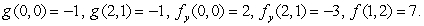
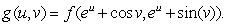 Find
Find 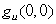 given that
given that 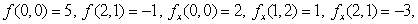 and
and 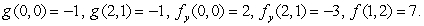

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
52
Find the equation of the tangent plane to the surface at (1, -3, 2).
A)
B)
C)
D)
A)
B)
C)
D)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
53
Suppose that as you move away from the point (-1, -1, -1), the function 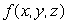 increases most rapidly in the direction
increases most rapidly in the direction 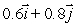 and the rate of increase of f in this direction is 4.At what rate is f increasing as you move away from (-1, -1, -1)in the direction of
and the rate of increase of f in this direction is 4.At what rate is f increasing as you move away from (-1, -1, -1)in the direction of 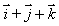 ? Give your answer to 4 decimal places.
? Give your answer to 4 decimal places.
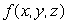 increases most rapidly in the direction
increases most rapidly in the direction 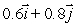 and the rate of increase of f in this direction is 4.At what rate is f increasing as you move away from (-1, -1, -1)in the direction of
and the rate of increase of f in this direction is 4.At what rate is f increasing as you move away from (-1, -1, -1)in the direction of 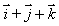 ? Give your answer to 4 decimal places.
? Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
54
Let w = 3x cos 4y.If 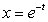 and
and 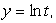 find
find 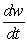 at the point t = 3.Give your answer to 2 decimal places.
at the point t = 3.Give your answer to 2 decimal places.
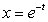 and
and 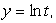 find
find 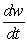 at the point t = 3.Give your answer to 2 decimal places.
at the point t = 3.Give your answer to 2 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
55
The quantity z can be expressed as a function of x and y as follows: z = f(x, y).Now x and y are themselves functions of r and , as follows: and Suppose you know that g(1, /2)= -1, and h(1, /2)= 1.In addition, you are told that Find

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
56
Let w = 3x cos y.If find w/ u and w/ v at the point .Give your answers to 2 decimal places.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
57
Find the directional derivative of 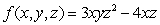 at the point (3, 3, 2), in the direction of the vector
at the point (3, 3, 2), in the direction of the vector 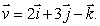
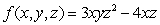 at the point (3, 3, 2), in the direction of the vector
at the point (3, 3, 2), in the direction of the vector 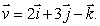

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
58
Below is a contour diagram for f(x, y)which is defined and continuous everywhere.The z-values have been omitted.Explain why it is true that . 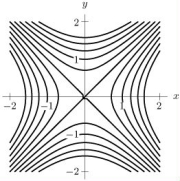


Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
59
Sally is on a day hike at Mt.Baker.From 9 to 11:00 a.m.she zig-zags up z = f(x, y)where x is the number of miles due east of her starting position, y is the number of miles due north of her starting position, and z is her elevation in miles above sea level.Feeling tired, she decides to continue walking, but in such a way that her altitude remains constant from 11 a.m.to noon to settle her stomach for lunch.At 11:30 a.m., she will be passing through (2, -1, 5)where fx(2, -1)= 3 and fy(2, -1)= -2.
What is the slope of her "path" in the x, y plane at this instant? (This "path" is among the level curves in the plane.)
What is the slope of her "path" in the x, y plane at this instant? (This "path" is among the level curves in the plane.)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
60
If you know the directional derivative of f(x, y)in two distinct directions (i.e.not including opposite directions)at a point P then you can find

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
61
Let 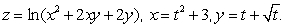 Find dz/dt at t = 1 using the chain rule.Give your answer to 4 decimal places.
Find dz/dt at t = 1 using the chain rule.Give your answer to 4 decimal places.
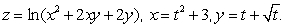 Find dz/dt at t = 1 using the chain rule.Give your answer to 4 decimal places.
Find dz/dt at t = 1 using the chain rule.Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
62
Find the angle between the vector 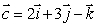 and the positive z-axis.
and the positive z-axis.
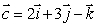 and the positive z-axis.
and the positive z-axis.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
63
Find the following partial derivative: fxy if .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
64
Given that 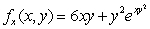 and
and 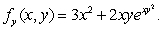 Suppose that f(1, 1)= 4.Find the quadratic Taylor polynomial of f(x, y)at (1, 1).
Suppose that f(1, 1)= 4.Find the quadratic Taylor polynomial of f(x, y)at (1, 1).
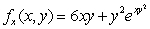 and
and 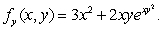 Suppose that f(1, 1)= 4.Find the quadratic Taylor polynomial of f(x, y)at (1, 1).
Suppose that f(1, 1)= 4.Find the quadratic Taylor polynomial of f(x, y)at (1, 1).
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
65
Using the contour diagram for f(x, y), find the sign of given that fxx(P)< 0. 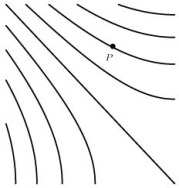
A)Negative
B)Positive
C)Not possible to decide

A)Negative
B)Positive
C)Not possible to decide

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
66
If 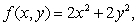 and
and 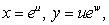 find fw(1, 1)using the chain rule.Give your answer to 4 decimal places.
find fw(1, 1)using the chain rule.Give your answer to 4 decimal places.
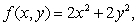 and
and 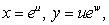 find fw(1, 1)using the chain rule.Give your answer to 4 decimal places.
find fw(1, 1)using the chain rule.Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
67
If 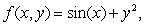 x(u, v)= uv and y(u, v)= u + 4v.
x(u, v)= uv and y(u, v)= u + 4v.
If H(u, v)= f(x(u, v), y(u, v)), what is H(0,-1)? Give your answer to 4 decimal places.
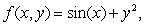 x(u, v)= uv and y(u, v)= u + 4v.
x(u, v)= uv and y(u, v)= u + 4v.If H(u, v)= f(x(u, v), y(u, v)), what is H(0,-1)? Give your answer to 4 decimal places.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
68
Suppose that fx(2, 1)= 2.2, fx(2.5, 1)= 1, fx(2, 1.5)= 1.8, fy(2, 1)= -0.8, fy(2.5, 1)= -1.2 and fy(2, 1.5)= -1.4.
If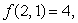 estimate the value of f(1.85, 0.8)using a quadratic Taylor polynomial about (2,1).
estimate the value of f(1.85, 0.8)using a quadratic Taylor polynomial about (2,1).
Use difference quotients to approximate all second derivatives.
If
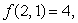 estimate the value of f(1.85, 0.8)using a quadratic Taylor polynomial about (2,1).
estimate the value of f(1.85, 0.8)using a quadratic Taylor polynomial about (2,1).Use difference quotients to approximate all second derivatives.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
69
If 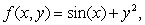 x(u, v)= uv and y(u, v)= u + 3v.
x(u, v)= uv and y(u, v)= u + 3v.
If H(u, v)= f(x(u, v), y(u, v)), what is Hv(0,-2)? Give your answer to 4 decimal places.
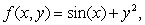 x(u, v)= uv and y(u, v)= u + 3v.
x(u, v)= uv and y(u, v)= u + 3v.If H(u, v)= f(x(u, v), y(u, v)), what is Hv(0,-2)? Give your answer to 4 decimal places.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
70
The table below gives values of a function f(x, y)near x = 1, y = 2. 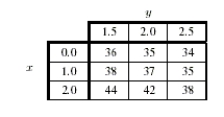 Give the equation of the tangent plane to the graph z = f(x, y)at x = 1, y = 2.
Give the equation of the tangent plane to the graph z = f(x, y)at x = 1, y = 2.
A)
B)
C)
D)
E)
 Give the equation of the tangent plane to the graph z = f(x, y)at x = 1, y = 2.
Give the equation of the tangent plane to the graph z = f(x, y)at x = 1, y = 2.A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
71
Find a unit vector perpendicular to both and .
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
72
Consider the function (a)Find gx(x, y)and gy(x, y)for (x, y) (0, 0).
(b)Use the limit definition of partial derivative to show that gx(0, 0)= 0 and gy(0, 0)= 0.
(c)Are the functions gx and gy continuous at (0, 0)? Explain.
(d)Is g differentiable at (0, 0)? Explain.
(b)Use the limit definition of partial derivative to show that gx(0, 0)= 0 and gy(0, 0)= 0.
(c)Are the functions gx and gy continuous at (0, 0)? Explain.
(d)Is g differentiable at (0, 0)? Explain.

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
73
Find the following partial derivative: HP(2, 1)if 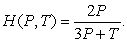 Give your answer to 4 decimal places.
Give your answer to 4 decimal places.
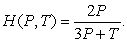 Give your answer to 4 decimal places.
Give your answer to 4 decimal places.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
74
The table below gives values of a function f(x, y)near x = 1, y = 2. 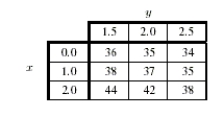 Estimate
Estimate 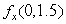 .
.
 Estimate
Estimate 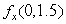 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
75
If fx(0, 0)exists and fy(0, 0)exists, then f is differentiable at (0, 0).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
76
Consider the level curves shown for the function z = f(x, y). 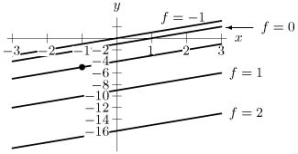 Determine the sign of
Determine the sign of
A)Positive
B)Negative
 Determine the sign of
Determine the sign of A)Positive
B)Negative

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
77
Suppose that 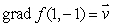 , with
, with 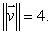 (a)What is the directional derivative of f at (1, -1)in the direction of
(a)What is the directional derivative of f at (1, -1)in the direction of 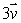 ?
?
(b)What is the smallest value of the directional derivative of f at (1, -1)among all possible directions?
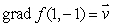 , with
, with 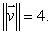 (a)What is the directional derivative of f at (1, -1)in the direction of
(a)What is the directional derivative of f at (1, -1)in the direction of 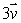 ?
?(b)What is the smallest value of the directional derivative of f at (1, -1)among all possible directions?

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
78
Find the directional derivative of 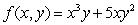 at the point (1, 1)in the direction of
at the point (1, 1)in the direction of 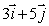 .
.
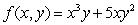 at the point (1, 1)in the direction of
at the point (1, 1)in the direction of 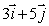 .
.
Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
79
Let f be a differentiable function with local linearization L(x, y)= -1 + 4(x - 4)- 2(y - 2)at (4, 2).Evaluate f(4, 2).

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck
80
Find the quadratic approximation to the function f(x, y)= cos x cos y valid near the origin.
A)
B)
C)
D)
E)
A)
B)
C)
D)
E)

Unlock Deck
Unlock for access to all 129 flashcards in this deck.
Unlock Deck
k this deck


