Exam 14: Differentiating Functions of Several Variables
Exam 1: A Library of Functions110 Questions
Exam 2: Key Concept: the Derivative92 Questions
Exam 3: Short-Cuts to Differentiation175 Questions
Exam 4: Using the Derivative108 Questions
Exam 5: Key Concept- the Definite Integral62 Questions
Exam 6: Constructing Antiderivatives90 Questions
Exam 7: Integration179 Questions
Exam 8: Using the Definite Integral104 Questions
Exam 9: Sequences and Series70 Questions
Exam 10: Approximating Functions Using Series71 Questions
Exam 11: Differential Equations135 Questions
Exam 12: Functions of Several Variables93 Questions
Exam 13: A Fundamental Tool- Vectors107 Questions
Exam 14: Differentiating Functions of Several Variables129 Questions
Exam 15: Optimization- Local and Global Extrema77 Questions
Exam 16: Integrating Functions of Several Variables76 Questions
Exam 17: Parameterization and Vector Fields86 Questions
Exam 18: Line Integrals78 Questions
Exam 19: Flux Integrals and Divergence52 Questions
Exam 20: The Curl and Stokes Theorem84 Questions
Exam 21: Parameters, Coordinates, Integrals23 Questions
Select questions type
What is the z-coordinate of the point if P lies on the plane which is tangent to the ellipsoid at the point ? Give your answer to four decimal places.
Free
(Essay)
4.8/5  (31)
(31)
Correct Answer:
The z-coordinate is .
Find the gradient of the function at the point and use the result to obtain a linear approximation for
Free
(Short Answer)
5.0/5  (35)
(35)
Correct Answer:
1.02
Let Use the appropriate partial derivative to find the slope of the cross-section at the given point.
(a)The cross-section f(x, 2)at the point (3, 2).
(b)The cross-section f(1, y)at the point (1, -2).
(Essay)
4.8/5  (29)
(29)
Given the contour diagram shown below, state whether is positive, negative or nearly zero. 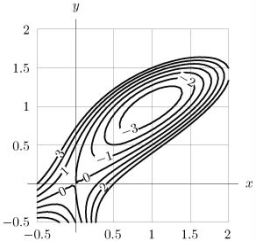
(Multiple Choice)
4.8/5  (30)
(30)
The ideal gas law states that for a fixed amount of gas, called a mole of gas, where P is the pressure (in atmospheres), V is the volume (in cubic meters), T is the temperature (in degrees Kelvin)and R is a positive constant.
Find
(Essay)
4.8/5  (32)
(32)
Suppose that as you move away from the point (-1, -1, -1), the function increases most rapidly in the direction and the rate of increase of f in this direction is 4.At what rate is f increasing as you move away from (-1, -1, -1)in the direction of ? Give your answer to 4 decimal places.
(Short Answer)
4.8/5  (31)
(31)
If and find fw(1, 1)using the chain rule.Give your answer to 4 decimal places.
(Essay)
4.9/5  (36)
(36)
An ant is walking along the surface which is the graph of the function (a)When the ant is at the point (1, 0, 1), what direction should it move in order to be moving on the surface in the direction of greatest ascent?
(b)If the ant moves in this direction at a speed of 6 units per second, what is the rate of change of height of the ant?
(Essay)
4.9/5  (31)
(31)
Suppose that the temperature at the point is given by .If you are at the point , in which direction should you go to decrease your temperature the fastest?
(Multiple Choice)
4.8/5  (39)
(39)
The table of some values of f(x, y)is given below.Find a local linearization of f at (1 , 2). 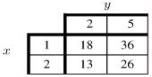
(Essay)
4.8/5  (32)
(32)
Suppose that the function and the linear function satisfy for points close to .Is f differentiable at (0,0)?
(Multiple Choice)
4.7/5  (33)
(33)
If you know the directional derivative of f(x, y)in two distinct directions (i.e.not including opposite directions)at a point P then you can find
(True/False)
4.9/5  (32)
(32)
The consumption of beef, C (in pounds per week per household)is given by the function C = f(I, p), where I is the household income in thousands of dollars per year, and p is the price of beef in dollars per pound.Explain the meaning of the statement: , and include units in your answer.
(Essay)
4.8/5  (40)
(40)
A rectangular beam, supported at its two ends, will sag when subjected to a uniform load.The amount of sag is calculated from the formula: , where p is the load (in Newtons per meter), x is the length between supports (in meters), w is the width of the beam (in meters), h is the height of the beam (in meters), and C is a constant (depending on material and units of measurement used).Determine for a beam 3 m long, 0.1 m wide, 0.2 m high subjected to a load of 80 N/m.
(Multiple Choice)
4.7/5  (29)
(29)
If $P is invested in a bank account earning r% interest a year, compounded continuously, the balance, $B, at the end of t years is given by Find
(Essay)
4.9/5  (25)
(25)
Let w = 3x cos 4y.If and find at the point t = 3.Give your answer to 2 decimal places.
(Essay)
4.8/5  (30)
(30)
Showing 1 - 20 of 129
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)