Deck 8: Estimating Single Population Parameters
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/174
Play
Full screen (f)
Deck 8: Estimating Single Population Parameters
1
Sampling error is the difference between a statistic computed from a sample and the corresponding parameter computed from the population.
True
2
The fact that a point estimate will likely be different from the corresponding population value is due to the fact that point estimates are subject to sampling error.
True
3
A report in a consumer magazine indicated that with 90 percent confidence, the mean number of hours that a particular brand light bulb lasts is between 900 and 1,100 hours. Based on this, the sample mean that produced this estimate is 1,000 hours.
True
4
In a recent report to the supply-chain manager in a major electronics company, the report writer stated that with 90 percent confidence, the manufacturing lead time for a critical part is between 3.34 hours and 4.14 hours. Based on this information, the margin of error for this estimate is ±.80 hours.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
5
The product manager for a large retail store has recently stated that she estimates that the average purchase per visit for the store's customers is between $33.00 and $65.00. The $33.00 and the $65.00 are considered point estimates for the true population mean.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
6
If a population is skewed, the point estimate will be pushed to the right or left of the middle of the confidence interval estimate.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
7
The higher the level of confidence, the wider the confidence interval must be.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
8
To construct a 99 percent confidence interval where σ is known, the correct critical value is 1.96.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
9
A 95 percent confidence interval estimate indicates that there is a 95 percent chance that the true population value will fall within the range defined by the upper and lower limits.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
10
A point estimate for a population mean lies exactly halfway between the outer and lower limits of its confidence interval estimate.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
11
A point estimate is an unbiased estimator of the true population value. However, error is associated with this estimate.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
12
When developing a confidence interval estimate, the confidence level is calculated based on the size of the sample and the population standard deviation.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
13
A random sample of 100 boxes of cereal had a sample mean weight of 396 grams. The standard deviation is known to be 5 grams. The upper end of the confidence interval for the mean is 405.8 grams.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
14
When using a 95 percent confidence interval for a mean, the area in the upper tail of the distribution that is outside the interval is 5 percent.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
15
A statement in the newspaper attributed to the leader of a local union stated that the average hourly wage for union members in the region is $13.35. He indicated that this number came from a survey of union members. If an estimate was developed with 95 percent confidence, we can safely conclude that this value is within 95 percent of the true population mean hourly wage.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
16
In a recent report to the supply-chain manager in a major electronics company, the report writer stated that with 90 percent confidence, the manufacturing lead time for a critical part is between 3.34 hours and 4.14 hours. Based on this, the sample mean that generated the confidence interval was 3.60.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
17
In a situation where we know the population standard deviation but wish to estimate the population mean using a 90 percent confidence interval, the critical value is z = ±1.645.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
18
To find a 98 percent confidence interval where the standard deviation is known, the correct z-value to use for the critical value is 2.33.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
19
Recently, a marketing research company reported that based on a random sample of 300 households the mean number of trips to a major shopping mall per month per household is 4.12 trips. This value is referred to as a parameter and is subject to sampling error.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
20
A point estimate is equally likely to be higher or lower than the population mean if the sampling is done using a statistical sampling procedure.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
21
A higher confidence level means that the point estimate for the population mean will be closer to the true population mean.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
22
The standard deviation for the checking account balances is assumed known to be $357.50. Recently, a bank manager was interested in estimating the mean balance. To do this, she selected a random sample of 81 accounts and found a mean balance of $1,347.20. At a 95 percent confidence level, the lower limit for the confidence interval is $646.50.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
23
A pilot sample is one that is used when a decision maker wishes to get an advance idea of what the mean of the population might be.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
24
If the population is not normally distributed, the t-distribution cannot be used.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
25
The makers of weight loss product are interested in estimating the mean weight loss for users of their product. To do this, they have selected a random sample of n = 9 people and have provided them with a supply of the product. After six months, the nine people had an average weight loss of 15.3 pounds with a standard deviation equal to 3.5 pounds. The upper limit for the 90 percent confidence interval estimate for the population mean is approximately 17.47 pounds.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
26
All of the factors that are needed to determine the required sample size are within the control of the decision maker.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
27
If we are interested in estimating the population mean based on a sample from a population for which we know neither the mean nor the standard deviation, the critical value will be a t value from the t- distribution.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
28
In developing a confidence interval estimate, the margin of error is directly dependent on the value of the point estimate.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
29
A 95 percent confidence interval estimate will have a margin of error that is approximately ±47.5 percent of the size of the population mean.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
30
One factor that plays an important part in determining what the needed sample size is when developing a confidence interval estimate is the level of confidence that you wish to use.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
31
The bottlers of a new fruit juice daily select a random sample of 12 bottles of the drink to estimate the mean quantity of juice in the bottles filled that day. On one such day, the following results were observed: 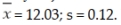 Based on this information, the upper limit for a 95 percent confidence interval estimate is approximately 12.106 ounces.
Based on this information, the upper limit for a 95 percent confidence interval estimate is approximately 12.106 ounces.
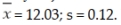 Based on this information, the upper limit for a 95 percent confidence interval estimate is approximately 12.106 ounces.
Based on this information, the upper limit for a 95 percent confidence interval estimate is approximately 12.106 ounces.
Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
32
One way to reduce the margin of error in a confidence interval estimate is to lower the level of confidence.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
33
The impact on the margin of error for a confidence interval for an increase in confidence level and a decrease in sample size is unknown since these changes are contradictory.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
34
The margin of error is one-half the width of the confidence interval.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
35
The bottlers of a new fruit juice daily select a random sample of 12 bottles of the drink to estimate the mean quantity of juice in the bottles filled that day. On one such day, the following results were observed: = 12.03; s = 0.12. Based on this information, the margin of error associated with a 90 percent confidence interval estimate for the population mean is 1.7959 ounces.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
36
A 95 percent confidence interval for a mean can be interpreted that we are 95 percent sure that our answer is correct.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
37
When calculating a confidence interval, the reason for using the t-distribution rather than the normal distribution for the critical value is that the population standard deviation is unknown.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
38
The t-distribution is used to obtain the critical value in developing a confidence interval when the population distribution is not known or the sample size is small.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
39
Confidence intervals constructed with small samples tend to have greater margins of error than those constructed from larger samples, all else being constant.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
40
In estimating a population mean, a large sample size is generally preferable to a small sample size because the margin of error is generally smaller.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
41
Two confidence interval estimates were developed from the same sample of a population. The wider interval will be the one that has the higher confidence level.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
42
If a decision maker desires a small margin of error and a high level of confidence, it is certain that the required sample size will be quite large.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
43
A grocery store manager is interested in estimating the mean weight of apples received in a shipment. If she wishes to have the estimate be within ±.05 pound with 90 percent confidence, the sample size should be 103 apples if she believes that the standard deviation is .08 pound.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
44
In estimating a population mean, increasing the confidence level will result in a higher margin of error for a given sample size.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
45
An emergency room in a hospital wants to determine the sample size needed for estimating their mean number of visits per day. If they want a 99 percent confidence level the correct critical value to use is 2.33.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
46
The main purpose of a pilot sample in an application involving an estimate for a population mean is to determine what the margin of error will likely be.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
47
An analyst for a financial investment firm recently went through the effort to determine the required sample size for estimating the mean number of transactions per year for the clients of his firm. The calculations, which were based on a 95 percent confidence level and a margin of error of ±3, gave a required sample size of 300. Given this information, the value used for the population standard deviation must have been about 26.5 transactions.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
48
If a pilot sample of n = 40 items has been used as a first step in determining a required sample size of n = 360, the decision maker can go ahead and use these 40 and take a sample of only 320 more items.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
49
In a sample size determination situation, reducing the margin of error by half will double the required sample size.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
50
In an effort to estimate the mean length of stay for motel guests at a major national motel chain, the decision makers asked for a 95 percent confidence, and a margin of error of ±0.25 days. Further, it was known that the population standard deviation is 0.50 days. Given this, the required sample size to estimate the mean length of stay is about 16 customers.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
51
The State Transportation Department wishes to estimate the mean speed of vehicles on a certain stretch of highway. They wish to estimate the mean within ±0.75 mph and they wish to have a confidence level equal to 99 percent. Based on this information only, they can determine that the required sample size is 320 vehicles.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
52
The national sales manager for a textbook publishing company wishes to estimate the mean number of books sold per college. She wishes to have her estimate be within ± 30 copies and wants a 95 percent confidence interval estimate. If a pilot sample of 30 schools gave a sample standard deviation equal to 60 books, the required total sample size is less than the pilot sample already taken.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
53
The manager in charge of concessions at an NFL football stadium is interested in estimating the mean dollars that are spent per person attending the games. A pilot sample of n = 50 people has revealed a sample mean and standard deviation of $12.35 and $2.35 respectively. He wishes to estimate the population mean within ± $0.20 of the true mean and wishes to have a confidence level of 95 percent. Given this, he needs to sample an additional 481 people.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
54
When finding sample size, cutting the margin of error in half requires that the sample size be four times larger.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
55
A bank manager wishes to estimate the mean waiting time spent by customers at his bank. He knows from previous experience that the standard deviation is about 4.0 minutes. If he desires a 90 percent confidence interval estimate and wishes to have a margin of error of 1 minute, the required sample size will be approximately 143.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
56
When estimating sample size, a 90 percent confidence level will result in a smaller sample size than a 95 percent confidence level.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
57
In determining the required sample size in an application involving an estimate for the population mean, if the population standard deviation is known, there is no compelling reason to select a pilot sample.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
58
After taking a speed-reading course, students are supposed to be able to read faster than they could before taking the course. A pilot sample of n = 25 students showed a mean increase of 300 words per minute with a standard deviation equal to 60 words per minute. To estimate the population mean with 95 percent confidence and a margin of error of ±10 minutes, the required sample size is approximately 139 students.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
59
When a decision maker determines the required sample size for estimating a population mean, a change in the confidence level will result in a change in the required sample size, provided that the margin of error is also modified accordingly.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
60
A university computer lab manager wishes to estimate the mean time that students stay in the lab per visit. She believes that the population standard deviation would be no larger than 10 minutes. Further, she wishes to have a confidence level of 90 percent and a margin of error of ±2.00 minutes. Given this, the sample size that she uses is approximately 60 students.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
61
The t-distribution is used for the critical value when estimating a population proportion when the standard deviation of the population is not known.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
62
A random sample of n = 500 people was surveyed recently to determine an estimate for the proportion of people in the population who had attended at least some college. The estimate concluded that between 0.357 and 0.443 of the population had attended. Given this information, we can determine that the confidence level was approximately 95 percent.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
63
The manager of the local county fair believes that no more than 30 percent of the adults in the county would object to a fee increase to attend the fair if it meant that better entertainment could be secured. To estimate the true proportion, he has selected a random sample of 200 adults. The manager will use a 90 percent confidence level. Assuming his assumption about the 30 percent holds, the margin of error for the estimate will be approximately ±.169.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
64
A local pizza company is interested in estimating the percentage of customers who would take advantage of a coupon offer. To do this, they give the coupon out to a random sample of 100 customers. Of these, 45 actually use the coupon. Based on a 95 percent confidence level, the upper and lower confidence interval limits are approximately 0.3525 to 0.5475.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
65
When determining sample size for a proportion, using p = 0.5 will produce the smallest possible value for n.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
66
A random sample of 100 people was selected from a population of customers at a local bank. The mean age of these customers was 40. If the population standard deviation is thought to be 5 years, the margin of error for a 95 percent confidence interval estimate is .98 year.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
67
In estimating a population proportion, the factors that are needed to determine the required sample size are the confidence level, the margin of error and some idea of what the population proportion is.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
68
A publisher is interested in estimating the proportion of textbooks that students resell at the end of the semester. He is interested in making this estimate using a confidence level of 95 percent and a margin of error of ±0.02. Based upon his prior experience, he believes that π is somewhere around 0.60. Given this information, the required sample size is over 2,300 students.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
69
When determining the sample size for a proportion, if you have no previous information available to estimate p, then the best value to use is π = 0.5.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
70
A local pizza company is interested in estimating the percentage of customers who would take advantage of a coupon offer. To do this, they give the coupon out to a random sample of 100 customers. Of these, 45 actually use the coupon. At the 95 percent confidence level it would be appropriate for the manager to conclude that possibly as many as 50 percent of his customers will redeem the coupon.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
71
For a given sample size and a given confidence level, the closer p is to 1.0, the greater the margin of error will be.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
72
Recently, a report in a financial journal indicated that the 90 percent confidence interval estimate for the proportion of investors who own one or more mutual funds is between 0.88 and 0.92. Given this information, the sample size that was used in this study was approximately 609 investors.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
73
The procurement manager for a large company wishes to estimate the proportion of parts from a supplier that are defective. She has selected a random sample of n = 200 incoming parts and has found 11 to be defective. Based on a 95 percent confidence level, the upper and lower limits for the confidence interval estimate are approximately 0.0234 to 0.0866.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
74
In determining the required sample size when estimating a population proportion, it is necessary to start with some idea of what that proportion is.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
75
When σ is unknown, one should use an estimate that is considered to be at least as large as the true σ. This will provide a conservative sample size to be on the safe side.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
76
The concept of margin of error applies directly when estimating a population mean, but is not appropriate when estimating a population proportion.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
77
In determining the sample size requirement for an application involving the estimation of the proportion of department store customers who pay using the store's credit card, the closer the true proportion is to .5, the larger will be the required sample size for a given margin of error and confidence level.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
78
A Parks and Recreation official surveyed 200 people at random who have used one of the city's parks. The survey revealed that 26 resided outside the city limits. If she had to arrive at one single value to estimate the true proportion of park users who are residents of the city it would be 0.13.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
79
The one sure thing that can be said about a point estimate is that it will most likely be subject to sampling error and not equal the parameter.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck
80
Chicago Connection, a local pizza company, delivers pizzas for free within the market area. The delivery drivers are paid $2.00 per delivery plus they get to keep any tips. To estimate the proportion of deliveries that result in a tip to the driver, a random sample of 64 deliveries was selected. Of these, 48 times a tip was received. Based on this information, and using a 95 percent confidence level, the upper limit for the confidence interval estimate is about .1061.

Unlock Deck
Unlock for access to all 174 flashcards in this deck.
Unlock Deck
k this deck


