Exam 8: Estimating Single Population Parameters
Exam 1: The Where, Why, and How of Data Collection167 Questions
Exam 2: Graphs, Charts and Tablesdescribing Your Data138 Questions
Exam 3: Describing Data Using Numerical Measures138 Questions
Exam 4: Introduction to Probability125 Questions
Exam 5: Discrete Probability Distributions161 Questions
Exam 6: Introduction to Continuous Probability Distributions122 Questions
Exam 7: Introduction to Sampling Distributions136 Questions
Exam 8: Estimating Single Population Parameters174 Questions
Exam 9: Introduction to Hypothesis Testing183 Questions
Exam 10: Estimation and Hypothesis Testing for Two Population Parameters121 Questions
Exam 11: Hypothesis Tests and Estimation for Population Variances69 Questions
Exam 12: Analysis of Variance162 Questions
Exam 13: Goodness-Of-Fit Tests and Contingency Analysis105 Questions
Exam 14: Introduction to Linear Regression and Correlation Analysis139 Questions
Exam 15: Multiple Regression Analysis and Model Building148 Questions
Exam 16: Analyzing and Forecasting Time-Series Data131 Questions
Exam 17: Introduction to Nonparametric Statistics103 Questions
Exam 18: Introducing Business Analytics48 Questions
Exam 19: Introduction to Decision Analysis48 Questions
Exam 20: Introduction to Quality and Statistical Process Control42 Questions
Select questions type
A university computer lab manager wishes to estimate the mean time that students stay in the lab per visit. She believes that the population standard deviation would be no larger than 10 minutes. Further, she wishes to have a confidence level of 90 percent and a margin of error of ±2.00 minutes. Given this, the sample size that she uses is approximately 60 students.
Free
(True/False)
4.8/5  (38)
(38)
Correct Answer:
False
The t-distribution is used to obtain the critical value in developing a confidence interval when the population distribution is not known or the sample size is small.
Free
(True/False)
4.9/5  (36)
(36)
Correct Answer:
True
The chamber of commerce in a beach resort town wants to estimate the proportion of visitors who are repeat visitors. From previous experience they believe the portion is in the vicinity of 0.5 and they want to estimate the proportion to within ± 0.03 percentage points with 95 percent confidence. The sample size they should use is:
Free
(Multiple Choice)
4.7/5  (44)
(44)
Correct Answer:
A
An educational organization in California is interested in estimating the mean number of minutes per day that children between the age of 6 and 18 spend watching television per day. A previous study showed that the population standard deviation was 21.5 minutes. The organization selected a random sample of n = 200 children between the ages of 6 and 18 and recorded the number of minutes of TV that each person watched on a particular day. The mean time was 191.3 minutes. If the leaders of the organization wish to develop an interval estimate with 98 percent confidence, what critical value should be used?
(Multiple Choice)
4.9/5  (44)
(44)
Construct a 95% confidence interval estimate for the population mean given the following values: 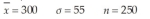
(Multiple Choice)
4.7/5  (29)
(29)
A 95 percent confidence interval estimate indicates that there is a 95 percent chance that the true population value will fall within the range defined by the upper and lower limits.
(True/False)
4.7/5  (25)
(25)
The bottlers of a new fruit juice daily select a random sample of 12 bottles of the drink to estimate the mean quantity of juice in the bottles filled that day. On one such day, the following results were observed: = 12.03; s = 0.12. Based on this information, the margin of error associated with a 90 percent confidence interval estimate for the population mean is 1.7959 ounces.
(True/False)
4.8/5  (32)
(32)
As the automobile accident rate increases, insurers are forced to increase their premium rates. Companies such as Allstate have recently been running a campaign they hope will result in fewer accidents by their policyholders. For each six-month period that a customer goes without an accident, Allstate will reduce the customer's premium rate by a certain percentage. Companies like Allstate have reason to be concerned about driving habits, based on a survey conducted by Drive for Life, a safety group sponsored by Volvo of North America, in which 1,100 drivers were surveyed. Among those surveyed, 74% said that careless or aggressive driving was the biggest threat on the road. One-third of the respondents said that cell phone usage by other drivers was the driving behavior that annoyed them the most. Based on these data, assuming that the sample was a simple random sample, construct and interpret a 95% confidence interval estimate for the true proportion in the population of all drivers who are annoyed by cell phone users.
(Multiple Choice)
4.8/5  (41)
(41)
The administrator at Sacred Heart Hospital is interested in estimating the proportion of patients who are satisfied with the meals at the hospital. A random sample of 250 patients was selected and the patients were surveyed. Of these, 203 indicated that they were satisfied. Based on this, what is the estimate of the standard error of the sampling distribution?
(Multiple Choice)
4.7/5  (38)
(38)
Determine the 90% confidence interval estimate for the population mean of a normal distribution 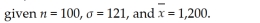
(Multiple Choice)
4.9/5  (31)
(31)
In developing a confidence interval estimate for the population mean, which of the following is true?
(Multiple Choice)
4.7/5  (39)
(39)
One factor that plays an important part in determining what the needed sample size is when developing a confidence interval estimate is the level of confidence that you wish to use.
(True/False)
4.8/5  (36)
(36)
Most major airlines allow passengers to carry two pieces of luggage (of a certain maximum size) onto the plane. However, their studies show that the more carry-on baggage passengers have, the longer it takes to unload and load passengers. One regional airline is considering changing its policy to allow only one carry-on per passenger. Before doing so, it decided to collect some data. Specifically, a random sample of 1,000 passengers was selected. The passengers were observed, and the number of bags carried on the plane was noted. Out of the 1,000 passengers, 345 had more than one bag. Based on this sample, develop and interpret a 95% confidence interval estimate for the proportion of the traveling population that would have been impacted had the one-bag limit been in effect.
(Multiple Choice)
4.8/5  (41)
(41)
In a recent audit report, an accounting firm stated that the mean sale per customer for the client was estimated to be between $14.50 and $28.50. Further, this was based on a random sample of 100 customers and was computed using 95 percent confidence. Provide a correct interpretation of this confidence interval estimate.
(Essay)
4.9/5  (39)
(39)
A decision maker is interested in estimating a population proportion. A sample of size n = 150 yields 115 successes. Based on these sample data, construct a 90% confidence interval estimate for the true population proportion.
(Multiple Choice)
4.9/5  (37)
(37)
If we are interested in estimating the population mean based on a sample from a population for which we know neither the mean nor the standard deviation, the critical value will be a t value from the t- distribution.
(True/False)
4.8/5  (34)
(34)
A publisher is interested in estimating the proportion of textbooks that students resell at the end of the semester. He is interested in making this estimate using a confidence level of 95 percent and a margin of error of ±0.02. Based upon his prior experience, he believes that π is somewhere around 0.60. Given this information, the required sample size is over 2,300 students.
(True/False)
4.9/5  (34)
(34)
In developing a confidence interval estimate for the population mean, the t-distribution is used to obtain the critical value when:
(Multiple Choice)
4.8/5  (34)
(34)
Suppose that an internal report submitted to the managers at a bank in Boston showed that with 95 percent confidence, the proportion of the bank's customers who also have accounts at one or more other banks is between .45 and .51. Given this information, what sample size was used to arrive at this estimate?
(Multiple Choice)
4.9/5  (33)
(33)
The product manager for a large retail store has recently stated that she estimates that the average purchase per visit for the store's customers is between $33.00 and $65.00. The $33.00 and the $65.00 are considered point estimates for the true population mean.
(True/False)
4.8/5  (35)
(35)
Showing 1 - 20 of 174
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)