Deck 6: Set Theory
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/19
Play
Full screen (f)
Deck 6: Set Theory
1
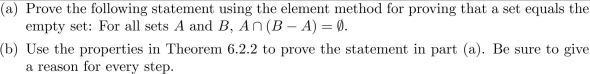
 20
20 
2
Consider the statement ![Consider the statement Complete the proof begun below in which the given statement is derived algebraically from the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly justifies what was done in the step: which is the right-hand side of the equation to be shown. [Hence the given statement is true.] (The number of lines in the outline shown above works for one version of a proof. If you write a proof using more or fewer lines, be sure to follow the given format, supplying a reason for every step that exactly justifies what was done in the step.)](https://storage.examlex.com/TB7212/11eb4916_5841_13c3_b114_6562960edd76_TB7212_00.jpg)
Complete the proof begun below in which the given statement is derived algebraically from
the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly
justifies what was done in the step:![Consider the statement Complete the proof begun below in which the given statement is derived algebraically from the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly justifies what was done in the step: which is the right-hand side of the equation to be shown. [Hence the given statement is true.] (The number of lines in the outline shown above works for one version of a proof. If you write a proof using more or fewer lines, be sure to follow the given format, supplying a reason for every step that exactly justifies what was done in the step.)](https://storage.examlex.com/TB7212/11eb4916_5841_13c4_b114_dbbf6f2ed1ef_TB7212_00.jpg)
which is the right-hand side of the equation to be shown. [Hence the given statement is true.]
(The number of lines in the outline shown above works for one version of a proof. If you write
a proof using more or fewer lines, be sure to follow the given format, supplying a reason for
every step that exactly justifies what was done in the step.)
![Consider the statement Complete the proof begun below in which the given statement is derived algebraically from the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly justifies what was done in the step: which is the right-hand side of the equation to be shown. [Hence the given statement is true.] (The number of lines in the outline shown above works for one version of a proof. If you write a proof using more or fewer lines, be sure to follow the given format, supplying a reason for every step that exactly justifies what was done in the step.)](https://storage.examlex.com/TB7212/11eb4916_5841_13c3_b114_6562960edd76_TB7212_00.jpg)
Complete the proof begun below in which the given statement is derived algebraically from
the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly
justifies what was done in the step:
![Consider the statement Complete the proof begun below in which the given statement is derived algebraically from the properties listed in Theorem 6.2.2. Be sure to give a reason for every step that exactly justifies what was done in the step: which is the right-hand side of the equation to be shown. [Hence the given statement is true.] (The number of lines in the outline shown above works for one version of a proof. If you write a proof using more or fewer lines, be sure to follow the given format, supplying a reason for every step that exactly justifies what was done in the step.)](https://storage.examlex.com/TB7212/11eb4916_5841_13c4_b114_dbbf6f2ed1ef_TB7212_00.jpg)
which is the right-hand side of the equation to be shown. [Hence the given statement is true.]
(The number of lines in the outline shown above works for one version of a proof. If you write
a proof using more or fewer lines, be sure to follow the given format, supplying a reason for
every step that exactly justifies what was done in the step.)

3
Disprove the following statement by finding a counterexample. 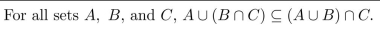
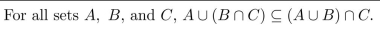
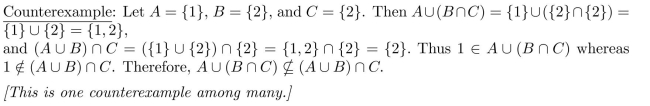
4
Derive the following result "algebraically" using the properties listed in Theorem 6.2.2. Give
a reason for every step that exactly justifies what was done in the step.
a reason for every step that exactly justifies what was done in the step.


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
5
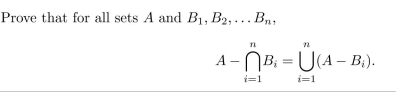

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
6
Write a negation for the following statement: 


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
7
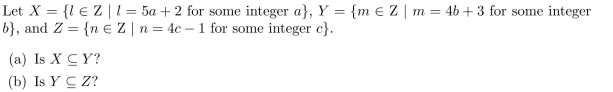
Justify your answers carefully. (In other words, provide a proof if the statement is true or a
disproof if the statement is false.)

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
8
Derive the following result. You may do so either "algebraically" using the properties listed in
Theorem 6.2.2, being sure to give a reason for every step, or you may use the element method
for proving a set equals the empty set.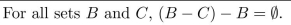
Theorem 6.2.2, being sure to give a reason for every step, or you may use the element method
for proving a set equals the empty set.
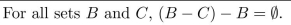

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
9
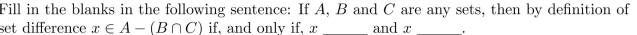

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
10
Consider the statement 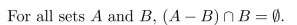
The proof below is the beginning of a proof using the element method for proving that the
set equals the empty set. Complete the proof without using any of the set properties from
Theorem 6.2.2.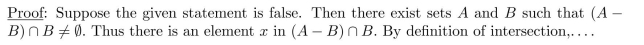
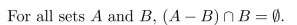
The proof below is the beginning of a proof using the element method for proving that the
set equals the empty set. Complete the proof without using any of the set properties from
Theorem 6.2.2.
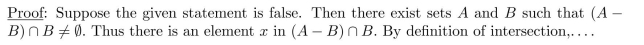

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
11
Is the following sentence a statement: This sentence is false or 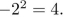
Justify your answer.
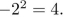
Justify your answer.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
12
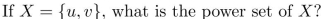

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
13


Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
14
Let A and B be sets. Define precisely (but concisely) what it means for A to be a subset of B.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
15
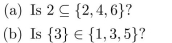

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
16
Use the element method for proving a set equals the empty set to prove that 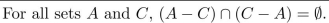
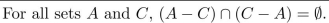

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
17
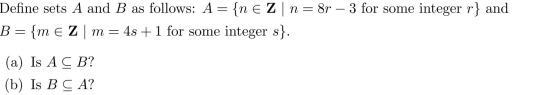
Justify your answers carefully. (In other words, provide a proof if the statement is true or a
disproof if the statement is false.)

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
18
Fill in the blanks: 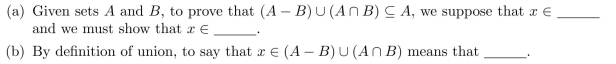

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck
19
Prove the following statement using an element argument and reasoning directly from the
definitions of union, intersection, set difference.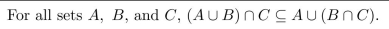
definitions of union, intersection, set difference.

Unlock Deck
Unlock for access to all 19 flashcards in this deck.
Unlock Deck
k this deck


