Deck 12: Boolean Algebra
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/11
Play
Full screen (f)
Deck 12: Boolean Algebra
1
Use a K-map to minimize the sum-of-products expansion x y z + x y z + x y z + x y z.
We construct the following K-map. 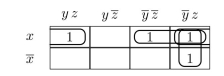 Combining terms gives us the expansion
Combining terms gives us the expansion 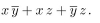
 Combining terms gives us the expansion
Combining terms gives us the expansion 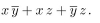
2
What is the output of the following circuit? 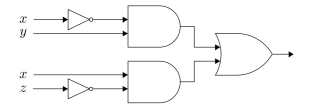

The output of the circuit is 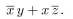
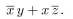
3
Prove or disprove that x y + y = y whenever x and y are Boolean variables.
When y = 1 we have x y + y = x + 1 = 1 = y. When y = 0 we have x y + y = x · 0 + 0 = 0 + 0 = 0 = y. Hence x y + y = y for all values of the Boolean variables x and y.
4
Use a K-map to minimize the sum-of-products expansion 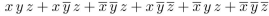
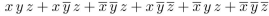

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
5
Find the sum-of-products expansion of a Boolean function f(x, y, z) that is 1 if and only if x = y = 1 and z = 0, or x = 0 and y = z = 1, or x = y = 0 and z = 1.

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
6
Find a Boolean function f(x, y, z) that has the value 1 if and only if exactly two of x, y, and z have the value 1.

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
7
What is the value of the Boolean function 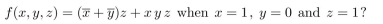

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
8
How many different Boolean functions are there of degree 3?

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
9
Is the set of operators {+, ·} functionally complete? Justify your answer.

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
10
Prove or disprove that 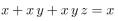 whenever x, y, and z are Boolean variables.
whenever x, y, and z are Boolean variables.
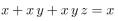 whenever x, y, and z are Boolean variables.
whenever x, y, and z are Boolean variables.
Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck
11
Construct a circuit using inverters, OR gates, and AND gates that gives an output of 1 if three people on a committee do not all vote the same.

Unlock Deck
Unlock for access to all 11 flashcards in this deck.
Unlock Deck
k this deck


