Deck 2: Motion Along a Straight Line
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/55
Play
Full screen (f)
Deck 2: Motion Along a Straight Line
1
Addition and subtraction: For the vectors shown in the figure, express vector 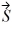 in terms of vectors
in terms of vectors  and
and  .
. 
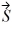 in terms of vectors
in terms of vectors 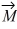 and
and 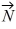 .
. 
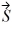 =
= 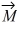 -
- 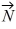
2
Components: Which of the following is an accurate statement?
A) The magnitude of a vector can be zero even though one of its components is not zero.
B) It is possible to add a scalar quantity to a vector.
C) Even though two vectors have unequal magnitudes, it is possible that their vector sum is zero.
D) Rotating a vector about an axis passing through the tip of the vector does not change the vector.
E) The magnitude of a vector is independent of the coordinate system used.
A) The magnitude of a vector can be zero even though one of its components is not zero.
B) It is possible to add a scalar quantity to a vector.
C) Even though two vectors have unequal magnitudes, it is possible that their vector sum is zero.
D) Rotating a vector about an axis passing through the tip of the vector does not change the vector.
E) The magnitude of a vector is independent of the coordinate system used.
The magnitude of a vector is independent of the coordinate system used.
3
Addition and subtraction: A rabbit trying to escape a fox runs north for 8.0 m, darts northwest for 1.0 m, then drops 1.0 m down a hole into its burrow. What is the magnitude of the net displacement of the rabbit?
A) 8.8 m
B) 8.1 m
C) 66 m
D) 10 m
A) 8.8 m
B) 8.1 m
C) 66 m
D) 10 m
8.8 m
4
Vector (cross) product: If two vectors are perpendicular to each other, their cross product must be zero.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
5
Scalar (dot) product: The value of the dot product of two vectors depends on the particular coordinate system being used.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
6
Unit vectors: If all the components of a vector are equal to 1, then that vector is a unit vector.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
7
Addition and subtraction: You walk 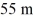 to the north, then turn 60° to your right and walk another
to the north, then turn 60° to your right and walk another 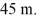 How far are you from where you originally started?
How far are you from where you originally started?
A) 87 m
B) 50 m
C) 94 m
D) 46 m
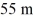 to the north, then turn 60° to your right and walk another
to the north, then turn 60° to your right and walk another 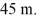 How far are you from where you originally started?
How far are you from where you originally started?A) 87 m
B) 50 m
C) 94 m
D) 46 m

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
8
Addition and subtraction: Under what condition is | 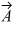 -
- 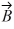 | = A + B?
| = A + B?
A) The magnitude of vector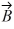 is zero.
is zero.
B) Vectors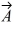 and
and
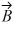 are in opposite directions.
are in opposite directions.
C) Vectors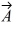 and
and
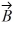 are in the same direction.
are in the same direction.
D) Vectors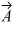 and
and
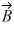 are in perpendicular directions.
are in perpendicular directions.
E) The statement is never true.
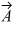 -
- 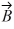 | = A + B?
| = A + B?A) The magnitude of vector
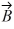 is zero.
is zero.B) Vectors
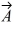 and
and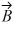 are in opposite directions.
are in opposite directions.C) Vectors
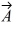 and
and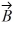 are in the same direction.
are in the same direction.D) Vectors
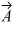 and
and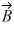 are in perpendicular directions.
are in perpendicular directions.E) The statement is never true.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
9
Vector (cross) product: If 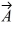 and
and 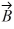 are nonzero vectors for which
are nonzero vectors for which 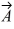 ∙
∙ 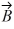 = 0, it must follow that
= 0, it must follow that
A)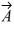 ×
×
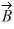 = 0.
= 0.
B)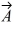 is parallel to
is parallel to
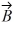 .
.
C) |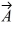 ×
×
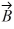 | = AB.
| = AB.
D) |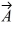 ×
×
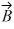 | = 1.
| = 1.
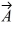 and
and 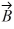 are nonzero vectors for which
are nonzero vectors for which 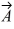 ∙
∙ 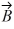 = 0, it must follow that
= 0, it must follow thatA)
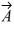 ×
×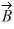 = 0.
= 0.B)
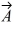 is parallel to
is parallel to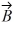 .
.C) |
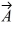 ×
×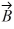 | = AB.
| = AB.D) |
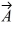 ×
×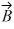 | = 1.
| = 1.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
10
Components: If the magnitude of vector 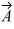 is less than the magnitude of vector
is less than the magnitude of vector 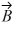 , then the x component of
, then the x component of 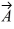 is always less than the x component of
is always less than the x component of 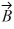 .
.
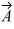 is less than the magnitude of vector
is less than the magnitude of vector 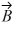 , then the x component of
, then the x component of 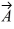 is always less than the x component of
is always less than the x component of 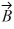 .
.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
11
Vector (cross) product: If two vectors point in opposite directions, their cross product must be zero.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
12
Scalar (dot) product: If two nonzero vectors point in the same direction, their dot product must be zero.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
13
Addition and subtraction: If 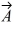 -
- 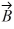 = 0, then the vectors
= 0, then the vectors 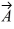 and
and 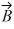 have equal magnitudes and are directed in the opposite directions from each other.
have equal magnitudes and are directed in the opposite directions from each other.
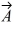 -
- 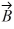 = 0, then the vectors
= 0, then the vectors 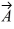 and
and 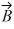 have equal magnitudes and are directed in the opposite directions from each other.
have equal magnitudes and are directed in the opposite directions from each other.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
14
Addition and subtraction: Vectors 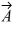 and
and 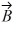 are shown in the figure. Vector
are shown in the figure. Vector 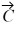 is given by
is given by 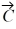 =
= 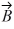 -
- 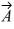 . The magnitude of vector
. The magnitude of vector 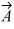 is 16.0 units, and the magnitude of vector
is 16.0 units, and the magnitude of vector 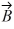 is 7.00 units. What is the angle of vector
is 7.00 units. What is the angle of vector 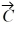 , measured counterclockwise from the +x-axis?
, measured counterclockwise from the +x-axis? 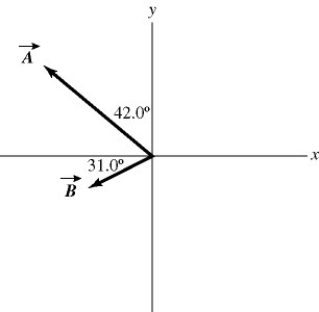
A) 16.9°
B) 22.4°
C) 73.1°
D) 287°
E) 292°
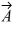 and
and 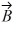 are shown in the figure. Vector
are shown in the figure. Vector 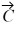 is given by
is given by 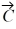 =
= 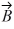 -
- 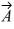 . The magnitude of vector
. The magnitude of vector 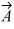 is 16.0 units, and the magnitude of vector
is 16.0 units, and the magnitude of vector 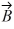 is 7.00 units. What is the angle of vector
is 7.00 units. What is the angle of vector 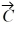 , measured counterclockwise from the +x-axis?
, measured counterclockwise from the +x-axis? 
A) 16.9°
B) 22.4°
C) 73.1°
D) 287°
E) 292°

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
15
Scalar (dot) product: If the dot product of two nonzero vectors is zero, the vectors must be perpendicular to each other.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
16
Addition and subtraction: You walk 53 m to the north, then turn 60° to your right and walk another 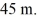 Determine the direction of your displacement vector. Express your answer as an angle relative to east.
Determine the direction of your displacement vector. Express your answer as an angle relative to east.
A) 63° N of E
B) 50° N of E
C) 57° N of E
D) 69° N of E
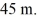 Determine the direction of your displacement vector. Express your answer as an angle relative to east.
Determine the direction of your displacement vector. Express your answer as an angle relative to east.A) 63° N of E
B) 50° N of E
C) 57° N of E
D) 69° N of E

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
17
Addition and subtraction: Vectors 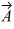 and
and 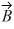 are shown in the figure. Vector
are shown in the figure. Vector 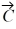 is given by
is given by 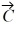 =
= 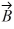 -
- 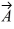 . The magnitude of vector
. The magnitude of vector 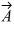 is 16.0 units, and the magnitude of vector
is 16.0 units, and the magnitude of vector  is 7.00 units. What is the magnitude of vector
is 7.00 units. What is the magnitude of vector  ?
? 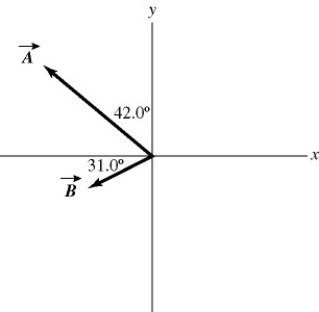
A) 9.00
B) 9.53
C) 15.5
D) 16.2
E) 17.5
 and
and 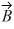 are shown in the figure. Vector
are shown in the figure. Vector 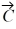 is given by
is given by 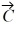 =
= 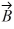 -
- 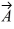 . The magnitude of vector
. The magnitude of vector 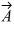 is 16.0 units, and the magnitude of vector
is 16.0 units, and the magnitude of vector 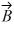 is 7.00 units. What is the magnitude of vector
is 7.00 units. What is the magnitude of vector 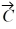 ?
? 
A) 9.00
B) 9.53
C) 15.5
D) 16.2
E) 17.5

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
18
Addition and subtraction: If A > B, under what condition is | 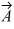 -
- 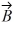 | = A - B?
| = A - B?
A) The statement is never true.
B) Vectors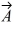 and
and
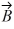 are in opposite directions.
are in opposite directions.
C) Vectors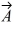 and
and
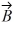 are in the same direction.
are in the same direction.
D) Vectors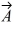 and
and
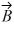 are in perpendicular directions.
are in perpendicular directions.
E) The statement is always true.
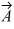 -
- 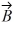 | = A - B?
| = A - B?A) The statement is never true.
B) Vectors
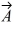 and
and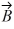 are in opposite directions.
are in opposite directions.C) Vectors
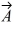 and
and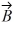 are in the same direction.
are in the same direction.D) Vectors
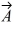 and
and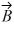 are in perpendicular directions.
are in perpendicular directions.E) The statement is always true.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
19
Components: The magnitude of a vector can never be less than the magnitude of one of its components.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
20
Components: If the eastward component of vector 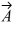 is equal to the westward component of vector
is equal to the westward component of vector 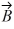 and their northward components are equal. Which one of the following statements about these two vectors is correct?
and their northward components are equal. Which one of the following statements about these two vectors is correct?
A) Vector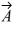 is parallel to vector
is parallel to vector
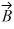 .
.
B) Vectors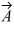 and
and
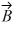 point in opposite directions.
point in opposite directions.
C) Vector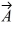 is perpendicular to vector
is perpendicular to vector
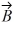 .
.
D) The magnitude of vector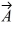 is equal to the magnitude of vector
is equal to the magnitude of vector
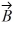 .
.
E) The magnitude of vector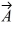 is twice the magnitude of vector
is twice the magnitude of vector
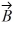 .
.
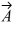 is equal to the westward component of vector
is equal to the westward component of vector 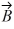 and their northward components are equal. Which one of the following statements about these two vectors is correct?
and their northward components are equal. Which one of the following statements about these two vectors is correct?A) Vector
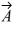 is parallel to vector
is parallel to vector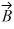 .
.B) Vectors
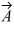 and
and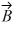 point in opposite directions.
point in opposite directions.C) Vector
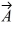 is perpendicular to vector
is perpendicular to vector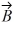 .
.D) The magnitude of vector
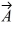 is equal to the magnitude of vector
is equal to the magnitude of vector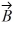 .
.E) The magnitude of vector
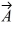 is twice the magnitude of vector
is twice the magnitude of vector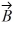 .
.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
21
Components: An airplane undergoes the following displacements: First, it flies 66 km in a direction 30° east of north. Next, it flies 49 km due south. Finally, it flies 100 km 30° north of west. Using vector components, determine how far the airplane ends up from its starting point.
A) 79 km
B) 81 km
C) 82 km
D) 78 km
E) 76 km
A) 79 km
B) 81 km
C) 82 km
D) 78 km
E) 76 km

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
22
Components: In the figure, the magnitude of vector 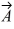 is 18.0 units, and the magnitude of vector
is 18.0 units, and the magnitude of vector 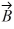 is 12.0 units. What vector
is 12.0 units. What vector 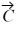 must be added to the vectors
must be added to the vectors 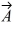 and
and 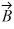 so that the resultant of these three vectors points in the -x direction and has a magnitude of 7.50 units? Use vector components to find your answer, and express vector
so that the resultant of these three vectors points in the -x direction and has a magnitude of 7.50 units? Use vector components to find your answer, and express vector 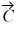 by giving its magnitude and the angle it makes with the +x-axis taking counterclockwise to be positive.
by giving its magnitude and the angle it makes with the +x-axis taking counterclockwise to be positive. 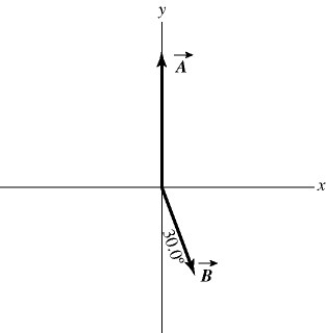
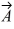 is 18.0 units, and the magnitude of vector
is 18.0 units, and the magnitude of vector 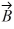 is 12.0 units. What vector
is 12.0 units. What vector 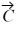 must be added to the vectors
must be added to the vectors 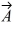 and
and 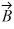 so that the resultant of these three vectors points in the -x direction and has a magnitude of 7.50 units? Use vector components to find your answer, and express vector
so that the resultant of these three vectors points in the -x direction and has a magnitude of 7.50 units? Use vector components to find your answer, and express vector 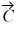 by giving its magnitude and the angle it makes with the +x-axis taking counterclockwise to be positive.
by giving its magnitude and the angle it makes with the +x-axis taking counterclockwise to be positive. 

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
23
Components: The components of vector 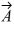 are Ax = + 3.90 and Ay = -4.00. What is the angle measured counterclockwise from the +x-axis to vector
are Ax = + 3.90 and Ay = -4.00. What is the angle measured counterclockwise from the +x-axis to vector 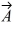 ?
?
A) 314°
B) 134°
C) 224°
D) 136°
E) 46.0°
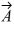 are Ax = + 3.90 and Ay = -4.00. What is the angle measured counterclockwise from the +x-axis to vector
are Ax = + 3.90 and Ay = -4.00. What is the angle measured counterclockwise from the +x-axis to vector 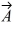 ?
?A) 314°
B) 134°
C) 224°
D) 136°
E) 46.0°

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
24
Components: Vector 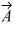 has a magnitude of 75.0 cm and points at 30° above the positive x-axis. Vector
has a magnitude of 75.0 cm and points at 30° above the positive x-axis. Vector 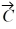 has a magnitude of 25.0 cm and points along the negative x-axis. Vector
has a magnitude of 25.0 cm and points along the negative x-axis. Vector 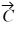 has a magnitude of 40.0 cm and points at 45° below the negative x-axis.
has a magnitude of 40.0 cm and points at 45° below the negative x-axis.
(a) Determine the x and y components of Vector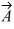 .
.
(b) Determine the x and y components of Vector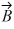 .
.
(c) Determine the x and y components of Vector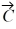 .
.
(d) Determine x and y components of the sum of these three vectors.
(e) Determine the magnitude and direction of the sum of these three vectors.
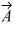 has a magnitude of 75.0 cm and points at 30° above the positive x-axis. Vector
has a magnitude of 75.0 cm and points at 30° above the positive x-axis. Vector 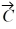 has a magnitude of 25.0 cm and points along the negative x-axis. Vector
has a magnitude of 25.0 cm and points along the negative x-axis. Vector 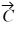 has a magnitude of 40.0 cm and points at 45° below the negative x-axis.
has a magnitude of 40.0 cm and points at 45° below the negative x-axis.(a) Determine the x and y components of Vector
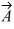 .
.(b) Determine the x and y components of Vector
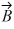 .
.(c) Determine the x and y components of Vector
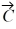 .
.(d) Determine x and y components of the sum of these three vectors.
(e) Determine the magnitude and direction of the sum of these three vectors.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
25
Components: A helicopter is flying horizontally with a speed of 444 m/s over a hill that slopes upward with a 2% grade (that is, the "rise" is 2% of the "run"). What is the component of the helicopter's velocity perpendicular to the sloping surface of the hill?
A) 8.9 m/s
B) 220 m/s
C) 435 m/s
D) 444 m/s
A) 8.9 m/s
B) 220 m/s
C) 435 m/s
D) 444 m/s

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
26
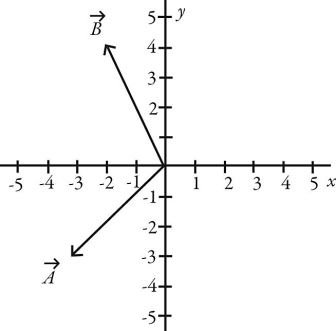
Unit vectors: Vectors 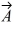 and
and 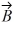 are shown in the figure. What is |-5.00
are shown in the figure. What is |-5.00 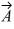 + 4.00
+ 4.00  |
| 
A) 31.8
B) -32.0 - 2.00
- 2.00

C) 1028
D) 34.0
E) -2.00 - 32.0
- 32.0

 and
and  are shown in the figure. What is |-5.00
are shown in the figure. What is |-5.00 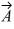 + 4.00
+ 4.00 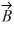 |
| 
A) 31.8
B) -32.0
 - 2.00
- 2.00
C) 1028
D) 34.0
E) -2.00
 - 32.0
- 32.0

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
27
Scalar (dot) product: Determine the scalar product of 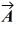 = 6.0
= 6.0  + 4.0
+ 4.0  - 2.0
- 2.0  and
and 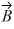 = 5.0
= 5.0  - 6.0
- 6.0  - 3.0
- 3.0 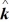 .
.
A) 30 + 24
+ 24
 + 6
+ 6
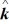
B) 30 - 24
- 24
 + 6
+ 6
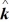
C) 12
D) 60
E) undefined
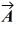 = 6.0
= 6.0  + 4.0
+ 4.0  - 2.0
- 2.0  and
and 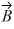 = 5.0
= 5.0  - 6.0
- 6.0  - 3.0
- 3.0 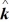 .
.A) 30
 + 24
+ 24 + 6
+ 6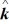
B) 30
 - 24
- 24 + 6
+ 6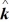
C) 12
D) 60
E) undefined

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
28
Components: As shown in the figure, three force vectors act on an object. The magnitudes of the forces as shown in the figure are F1 = 80.0 N, F2 = 60.0 N, and F3 = 40.0 N, where N is the standard SI unit of force. The resultant force acting on the object is given by 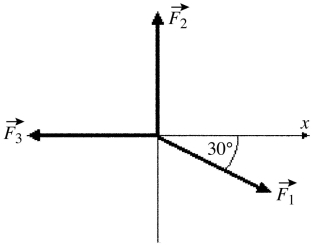
A) 180 N at an angle 60.0° with respect to +x-axis.
B) 60.0 N at an angle 90.0° with respect to +x-axis.
C) 20.0 N at an angle 34.3° with respect to +x-axis.
D) 35.5 N at an angle 34.3° with respect to +x-axis.
E) 40.0 N at an angle 60.0° with respect to +x-axis.

A) 180 N at an angle 60.0° with respect to +x-axis.
B) 60.0 N at an angle 90.0° with respect to +x-axis.
C) 20.0 N at an angle 34.3° with respect to +x-axis.
D) 35.5 N at an angle 34.3° with respect to +x-axis.
E) 40.0 N at an angle 60.0° with respect to +x-axis.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
29
Unit vectors: Vector 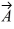 = 1.00
= 1.00  + -2.00
+ -2.00  and vector
and vector 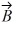 = 3.00
= 3.00  + 4.00
+ 4.00  What are the magnitude and direction of vector
What are the magnitude and direction of vector 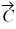 =
= 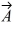 +
+ 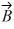 ?
?
A) 7.21 in a direction 33.7° counterclockwise from the positive x axis
B) 6.00 in a direction 63.4° counterclockwise from the positive x axis
C) 4.47 in a direction 6.34° counterclockwise from the positive x axis
D) 4.47 in a direction 26.6° counterclockwise from the positive x axis
E) 7.21 in a direction 56.3° counterclockwise from the positive x axis
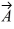 = 1.00
= 1.00  + -2.00
+ -2.00  and vector
and vector 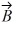 = 3.00
= 3.00  + 4.00
+ 4.00  What are the magnitude and direction of vector
What are the magnitude and direction of vector 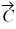 =
= 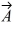 +
+ 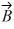 ?
?A) 7.21 in a direction 33.7° counterclockwise from the positive x axis
B) 6.00 in a direction 63.4° counterclockwise from the positive x axis
C) 4.47 in a direction 6.34° counterclockwise from the positive x axis
D) 4.47 in a direction 26.6° counterclockwise from the positive x axis
E) 7.21 in a direction 56.3° counterclockwise from the positive x axis

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
30
Components: The components of vector 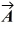 are
are 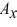 = + 2.2 and
= + 2.2 and 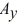 = -6.9 , and the components of vector
= -6.9 , and the components of vector 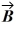 are given are
are given are 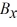 = -6.1 and
= -6.1 and 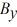 = -2.2. What is the magnitude of the vector
= -2.2. What is the magnitude of the vector 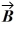 -
- 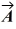 ?
?
A) 9.5
B) 6.1
C) 9.9
D) 91
E) 0.76
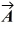 are
are 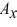 = + 2.2 and
= + 2.2 and 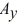 = -6.9 , and the components of vector
= -6.9 , and the components of vector 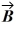 are given are
are given are 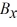 = -6.1 and
= -6.1 and 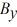 = -2.2. What is the magnitude of the vector
= -2.2. What is the magnitude of the vector 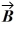 -
- 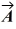 ?
?A) 9.5
B) 6.1
C) 9.9
D) 91
E) 0.76

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
31
Components: An apple falls from an apple tree growing on a 20° slope. The apple hits the ground with an impact velocity of 16.2 m/s straight downward. What is the component of the apple's impact velocity parallel to the surface of the slope?
A) 5.5 m/s
B) 8.7 m/s
C) 12 m/s
D) 15 m/s
A) 5.5 m/s
B) 8.7 m/s
C) 12 m/s
D) 15 m/s

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
32
Components: The components of vector 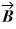 are
are 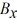 = -3.5 and
= -3.5 and 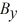 = -9.7, and the components of vector
= -9.7, and the components of vector 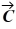 are
are 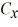 = -6 and
= -6 and 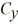 = + 8.1. What is the angle (less than 180 degrees) between vectors
= + 8.1. What is the angle (less than 180 degrees) between vectors 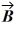 and
and 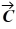 ?
?
A) 124°
B) 56°
C) 17°
D) 163°
E) 106°
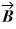 are
are 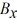 = -3.5 and
= -3.5 and 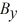 = -9.7, and the components of vector
= -9.7, and the components of vector 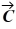 are
are 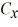 = -6 and
= -6 and 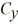 = + 8.1. What is the angle (less than 180 degrees) between vectors
= + 8.1. What is the angle (less than 180 degrees) between vectors 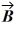 and
and 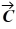 ?
?A) 124°
B) 56°
C) 17°
D) 163°
E) 106°

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
33
Unit vectors: If 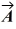 = + 4
= + 4  - 2
- 2  - 3
- 3 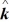 and
and 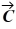 = - 4
= - 4  -2
-2  - 3
- 3 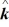 , which of the following numbers is closest to the magnitude of
, which of the following numbers is closest to the magnitude of 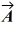 -
- 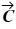 ?
?
A) 8
B) 7
C) 9
D) 10
E) 11
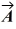 = + 4
= + 4  - 2
- 2  - 3
- 3 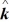 and
and 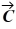 = - 4
= - 4  -2
-2  - 3
- 3 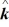 , which of the following numbers is closest to the magnitude of
, which of the following numbers is closest to the magnitude of 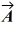 -
- 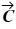 ?
?A) 8
B) 7
C) 9
D) 10
E) 11

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
34
Unit vectors: Vector 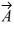 = -1.00
= -1.00  + -2.00
+ -2.00  and vector
and vector 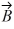 = 3.00
= 3.00  + 4.00
+ 4.00  What are the magnitude and direction of vector
What are the magnitude and direction of vector 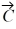 = 3.00
= 3.00 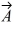 + 2.00
+ 2.00 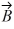 ?
?
A) 3.61 in a direction -56.3° counterclockwise from the positive x-axis
B) 3.61 in a direction 56.3° counterclockwise from the positive x-axis
C) 3.61 in a direction 33.7° counterclockwise from the positive x-axis
D) 5.00 in a direction 56.3° counterclockwise from the positive x axis
E) 6.72 in a direction 34.4° counterclockwise from the positive x-axis
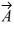 = -1.00
= -1.00  + -2.00
+ -2.00  and vector
and vector 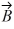 = 3.00
= 3.00  + 4.00
+ 4.00  What are the magnitude and direction of vector
What are the magnitude and direction of vector 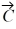 = 3.00
= 3.00  + 2.00
+ 2.00 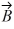 ?
?A) 3.61 in a direction -56.3° counterclockwise from the positive x-axis
B) 3.61 in a direction 56.3° counterclockwise from the positive x-axis
C) 3.61 in a direction 33.7° counterclockwise from the positive x-axis
D) 5.00 in a direction 56.3° counterclockwise from the positive x axis
E) 6.72 in a direction 34.4° counterclockwise from the positive x-axis

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
35
Components: Vector 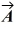 has a magnitude 5.00 and points in a direction 40.0° clockwise from the negative y axis. What are the x and y components of vector
has a magnitude 5.00 and points in a direction 40.0° clockwise from the negative y axis. What are the x and y components of vector 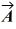 .
.
A) Ax = 3.83 and Ay = 3.21
B) Ax = 3.83 and Ay = -3.21
C) Ax = -3.21 and Ay = -3.83
D) Ax = -3.21 and Ay = 3.83
E) Ax = 4.29 and Ay = 2.16
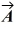 has a magnitude 5.00 and points in a direction 40.0° clockwise from the negative y axis. What are the x and y components of vector
has a magnitude 5.00 and points in a direction 40.0° clockwise from the negative y axis. What are the x and y components of vector 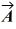 .
.A) Ax = 3.83 and Ay = 3.21
B) Ax = 3.83 and Ay = -3.21
C) Ax = -3.21 and Ay = -3.83
D) Ax = -3.21 and Ay = 3.83
E) Ax = 4.29 and Ay = 2.16

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
36
Components: Three forces are exerted on an object placed on a tilted floor. Forces are vectors. The three forces are directed as shown in the figure. If the forces have magnitudes 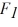 = 1.0 N,
= 1.0 N, 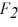 = 8.0 N and
= 8.0 N and 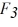 = 7.0 N, where N is the standard unit of force, what is the component of the net force
= 7.0 N, where N is the standard unit of force, what is the component of the net force 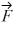 net =
net = 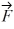
1 +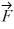
2 +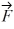
3 parallel to the floor?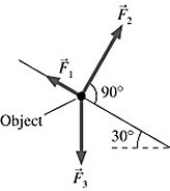
A) 2.5 N
B) 5.1 N
C) 6.0 N
D) 7.8 N
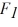 = 1.0 N,
= 1.0 N, 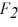 = 8.0 N and
= 8.0 N and 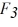 = 7.0 N, where N is the standard unit of force, what is the component of the net force
= 7.0 N, where N is the standard unit of force, what is the component of the net force 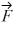 net =
net = 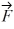
1 +
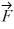
2 +
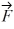
3 parallel to the floor?

A) 2.5 N
B) 5.1 N
C) 6.0 N
D) 7.8 N

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
37
Unit vectors: Vector 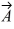 = -3.00
= -3.00  + 3.00
+ 3.00  and vector
and vector 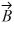 = 3.00
= 3.00  + 4.00
+ 4.00  . What is vector
. What is vector 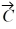 =
= 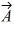 +
+ 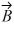 ?
?
A) 0.00 + 3.00
+ 3.00

B) 7.00 + 7.00
+ 7.00

C) -3.00 + 7.00
+ 7.00

D) 0.00 + 7.00
+ 7.00

E) -3.00 -3.00
-3.00

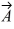 = -3.00
= -3.00  + 3.00
+ 3.00  and vector
and vector 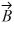 = 3.00
= 3.00  + 4.00
+ 4.00  . What is vector
. What is vector 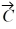 =
= 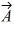 +
+ 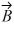 ?
?A) 0.00
 + 3.00
+ 3.00
B) 7.00
 + 7.00
+ 7.00
C) -3.00
 + 7.00
+ 7.00
D) 0.00
 + 7.00
+ 7.00
E) -3.00
 -3.00
-3.00

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
38
Components: A teacher sends her students on a treasure hunt. She gives the following instructions: 1. Walk 300 m north
2) Walk 400 m northwest
3) Walk 700 m east-southeast and the treasure is buried there.
As all the other students walk off following the instructions, Jane physics student quickly adds the displacements and walks in a straight line to find the treasure. How far and in what direction does Jane need to walk?
A) 187 m in a direction 67.3° north of east
B) 481 m in a direction 40.9° north of east
C) 399 m in a direction 52.5° north of east
D) 284 m in a direction 28.2° west of north
E) The treasure position cannot be reached in one straight walk.
2) Walk 400 m northwest
3) Walk 700 m east-southeast and the treasure is buried there.
As all the other students walk off following the instructions, Jane physics student quickly adds the displacements and walks in a straight line to find the treasure. How far and in what direction does Jane need to walk?
A) 187 m in a direction 67.3° north of east
B) 481 m in a direction 40.9° north of east
C) 399 m in a direction 52.5° north of east
D) 284 m in a direction 28.2° west of north
E) The treasure position cannot be reached in one straight walk.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
39
Unit vectors: What is the magnitude of 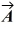 +
+ 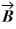 +
+ 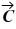 , where
, where 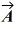 = 1.00
= 1.00  + 4.00
+ 4.00  - 1.00
- 1.00 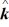 ,
, 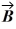 = 3.00
= 3.00  - 1.00
- 1.00  - 4.00
- 4.00 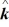 and
and 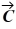 = -1.00
= -1.00  + 1.00
+ 1.00  ?
?
A) 7.07
B) 2.00
C) 10.76
D) 6.78
E) 8.12
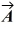 +
+ 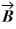 +
+ 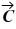 , where
, where 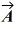 = 1.00
= 1.00  + 4.00
+ 4.00  - 1.00
- 1.00 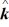 ,
, 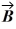 = 3.00
= 3.00  - 1.00
- 1.00  - 4.00
- 4.00 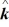 and
and 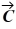 = -1.00
= -1.00  + 1.00
+ 1.00  ?
?A) 7.07
B) 2.00
C) 10.76
D) 6.78
E) 8.12

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
40
Components: Vector 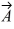 has a magnitude of 5.5 cm and points along the x-axis. Vector
has a magnitude of 5.5 cm and points along the x-axis. Vector 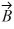 has a magnitude of 7.5 cm and points at +30° above the negative x-axis.
has a magnitude of 7.5 cm and points at +30° above the negative x-axis.
(a) Determine the x and y components of Vector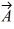 .
.
(b) Determine the x and y components of Vector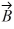 .
.
(c) Determine x and y components of the sum of these two vectors.
(d) Determine the magnitude and direction of the sum of these two vectors.
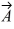 has a magnitude of 5.5 cm and points along the x-axis. Vector
has a magnitude of 5.5 cm and points along the x-axis. Vector 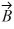 has a magnitude of 7.5 cm and points at +30° above the negative x-axis.
has a magnitude of 7.5 cm and points at +30° above the negative x-axis.(a) Determine the x and y components of Vector
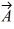 .
.(b) Determine the x and y components of Vector
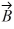 .
.(c) Determine x and y components of the sum of these two vectors.
(d) Determine the magnitude and direction of the sum of these two vectors.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
41
Vector (cross) product: If the magnitude of the cross product of two vectors is one-half the dot product of the same vectors, what is the angle between the two vectors?

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
42
Scalar (dot) product: The scalar product of vector 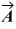 = 3.00
= 3.00  + 2.00
+ 2.00  and vector
and vector 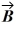 is 10.0. Which of the following vectors could be vector
is 10.0. Which of the following vectors could be vector 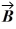 ?
?
A) 2.00 + 4.00
+ 4.00

B) 4.00 + 6.00
+ 6.00

C) 5.00 + 4.00
+ 4.00

D) 12.0
E) 2.00 + 2.00
+ 2.00

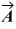 = 3.00
= 3.00  + 2.00
+ 2.00  and vector
and vector 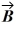 is 10.0. Which of the following vectors could be vector
is 10.0. Which of the following vectors could be vector 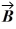 ?
?A) 2.00
 + 4.00
+ 4.00
B) 4.00
 + 6.00
+ 6.00
C) 5.00
 + 4.00
+ 4.00
D) 12.0

E) 2.00
 + 2.00
+ 2.00

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
43
Scalar (dot) product: If 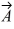 = 3
= 3  -
-  + 4
+ 4  and
and 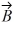 = x
= x  +
+  - 5
- 5  , find x so
, find x so  will be perpendicular to
will be perpendicular to  .
.
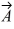 = 3
= 3  -
-  + 4
+ 4  and
and 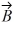 = x
= x  +
+  - 5
- 5  , find x so
, find x so 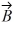 will be perpendicular to
will be perpendicular to 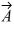 .
.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
44
Vector (cross) product: What is the vector product of 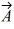 = 2.00
= 2.00  + 3.00
+ 3.00  + 1.00
+ 1.00  and
and 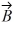 = 1.00
= 1.00  - 3.00
- 3.00  - 2.00
- 2.00  ?
?
A) -3.00 + 5.00
+ 5.00
 - 9.00
- 9.00

B) -5.00 + 2.00
+ 2.00
 - 6.00
- 6.00

C) -9.00 - 3.00
- 3.00
 - 3.00
- 3.00

D) -4.00 + 3.00
+ 3.00
 - 1.00
- 1.00

E) 2.00 - 9.00
- 9.00
 - 2.00
- 2.00

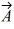 = 2.00
= 2.00  + 3.00
+ 3.00  + 1.00
+ 1.00  and
and 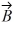 = 1.00
= 1.00  - 3.00
- 3.00  - 2.00
- 2.00  ?
?A) -3.00
 + 5.00
+ 5.00 - 9.00
- 9.00
B) -5.00
 + 2.00
+ 2.00 - 6.00
- 6.00
C) -9.00
 - 3.00
- 3.00 - 3.00
- 3.00
D) -4.00
 + 3.00
+ 3.00 - 1.00
- 1.00
E) 2.00
 - 9.00
- 9.00 - 2.00
- 2.00

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
45
Vector (cross) product: For the vectors shown in the figure, find the magnitude and direction of the vector product 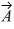 ×
×  that the quantities shown are accurate to two significant figures.
that the quantities shown are accurate to two significant figures. 
A) 16, directed into the plane
B) 16, directed out of the plane
C) 45, directed on the plane
D) 45, directed into the plane
E) 45, directed out of the plane
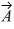 ×
× 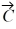 that the quantities shown are accurate to two significant figures.
that the quantities shown are accurate to two significant figures. 
A) 16, directed into the plane
B) 16, directed out of the plane
C) 45, directed on the plane
D) 45, directed into the plane
E) 45, directed out of the plane

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
46
Vector (cross) product: If 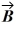 = -2
= -2  - 6
- 6  + 2
+ 2 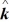 and
and 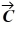 = - 2
= - 2  -2
-2  - 3
- 3 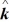 , which of the following numbers is closest to the magnitude of
, which of the following numbers is closest to the magnitude of 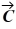 ×
× 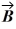 ?
?
A) 25
B) 21
C) 17
D) 13
E) 9
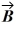 = -2
= -2  - 6
- 6  + 2
+ 2 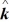 and
and 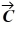 = - 2
= - 2  -2
-2  - 3
- 3 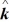 , which of the following numbers is closest to the magnitude of
, which of the following numbers is closest to the magnitude of 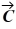 ×
× 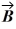 ?
?A) 25
B) 21
C) 17
D) 13
E) 9

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
47
Scalar (dot) product: What is the angle between the vector 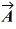 = + 3
= + 3  - 2
- 2  - 3
- 3 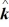 and the +y-axis?
and the +y-axis?
A) 115°
B) 65°
C) 25°
D) 155°
E) 90°
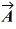 = + 3
= + 3  - 2
- 2  - 3
- 3 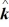 and the +y-axis?
and the +y-axis?A) 115°
B) 65°
C) 25°
D) 155°
E) 90°

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
48
Scalar (dot) product: The angle between vector 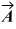 = 2.00
= 2.00  + 3.00
+ 3.00  and vector
and vector 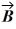 is
is 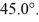 The scalar product of vectors
The scalar product of vectors 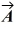 and
and 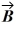 is 3.00. If the x component of vector
is 3.00. If the x component of vector 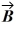 is positive, what is vector
is positive, what is vector 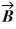 .
.
A)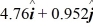
B)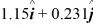
C)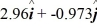
D)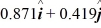
E)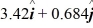
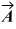 = 2.00
= 2.00  + 3.00
+ 3.00  and vector
and vector 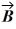 is
is 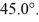 The scalar product of vectors
The scalar product of vectors 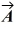 and
and 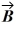 is 3.00. If the x component of vector
is 3.00. If the x component of vector 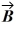 is positive, what is vector
is positive, what is vector 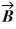 .
.A)
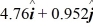
B)
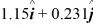
C)
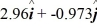
D)
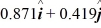
E)
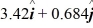

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
49
Scalar (dot) product: For the vectors shown in the figure, assume numbers are accurate to two significant figures. The scalar product  ×
×  is closest to
is closest to 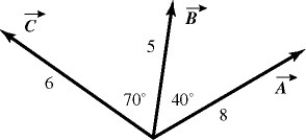
A) zero.
B) 16.
C) 45.
D) -16.
E) -45.
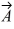 ×
× 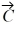 is closest to
is closest to 
A) zero.
B) 16.
C) 45.
D) -16.
E) -45.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
50
Scalar (dot) product: Determine the angle between the directions of vector 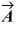 = 3.00
= 3.00  + 1.00
+ 1.00  and vector
and vector 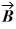 = -3.00
= -3.00  + 3.00
+ 3.00  .
.
A) 26.6°
B) 30.0°
C) 88.1°
D) 117°
E) 45.2°
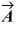 = 3.00
= 3.00  + 1.00
+ 1.00  and vector
and vector 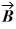 = -3.00
= -3.00  + 3.00
+ 3.00  .
.A) 26.6°
B) 30.0°
C) 88.1°
D) 117°
E) 45.2°

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
51
Vector (cross) product: If 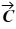 = - 4
= - 4  - 2
- 2  - 3
- 3 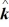 , what is
, what is 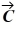 ×
×  ?
?
A) +3 - 4
- 4
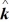
B) +3 + 4
+ 4
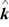
C) -3 + 4
+ 4
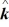
D) +3 + 2
+ 2
 - 4
- 4
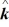
E) -3 - 2
- 2
 + 4
+ 4
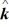
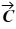 = - 4
= - 4  - 2
- 2  - 3
- 3 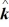 , what is
, what is 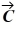 ×
×  ?
?A) +3
 - 4
- 4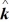
B) +3
 + 4
+ 4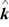
C) -3
 + 4
+ 4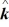
D) +3
 + 2
+ 2 - 4
- 4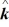
E) -3
 - 2
- 2 + 4
+ 4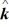

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
52
Vector (cross) product: What is the magnitude of the cross product of a vector of magnitude 2.00 m pointing east and a vector of magnitude 4.00 m pointing 30.0° west of north?
A) 6.93
B) -6.93
C) 4.00
D) -4.00
E) 8.00
A) 6.93
B) -6.93
C) 4.00
D) -4.00
E) 8.00

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
53
Scalar (dot) product: Two boys searching for buried treasure are standing underneath the same tree. One boy walks 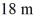 east and then
east and then 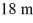 north. The other boy walks
north. The other boy walks 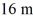 west and then
west and then 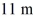 north. Find the scalar product of their net displacements from the tree.
north. Find the scalar product of their net displacements from the tree.
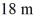 east and then
east and then 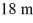 north. The other boy walks
north. The other boy walks 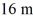 west and then
west and then 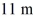 north. Find the scalar product of their net displacements from the tree.
north. Find the scalar product of their net displacements from the tree.
Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
54
Scalar (dot) product: A rectangular box is positioned with its vertices at the following points: A = (0,0,0) C = (2,4,0) E = (0,0,3) G = (2,4,3)
B = (2,0,0) D = (0,4,0) F = (2,0,3) H = (0,4,3)
If the coordinates all have three significant figures, the angle between the line segments AG and AH is closest to:
A) 21.8°.
B) 22.5°.
C) 26.6°.
D) 36.9°.
E) 45.0°.
B = (2,0,0) D = (0,4,0) F = (2,0,3) H = (0,4,3)
If the coordinates all have three significant figures, the angle between the line segments AG and AH is closest to:
A) 21.8°.
B) 22.5°.
C) 26.6°.
D) 36.9°.
E) 45.0°.

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck
55
Vector (cross) product: For the vectors shown in the figure, find the magnitude and direction of 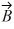 ×
× 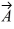 , assuming that the quantities shown are accurate to two significant figures.
, assuming that the quantities shown are accurate to two significant figures. 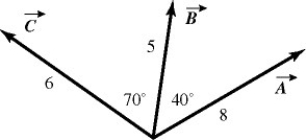
A) 26, directed into the plane
B) 26, directed out of the plane
C) 31, directed on the plane
D) 31, directed into the plane
E) 31, directed out of the plane
 ×
×  , assuming that the quantities shown are accurate to two significant figures.
, assuming that the quantities shown are accurate to two significant figures. 
A) 26, directed into the plane
B) 26, directed out of the plane
C) 31, directed on the plane
D) 31, directed into the plane
E) 31, directed out of the plane

Unlock Deck
Unlock for access to all 55 flashcards in this deck.
Unlock Deck
k this deck


