Exam 2: Motion Along a Straight Line
Exam 2: Motion Along a Straight Line55 Questions
Exam 3: Motion in Two or Three Dimensions59 Questions
Exam 4: Newtons Laws of Motion50 Questions
Exam 5: Applying Newtons Laws139 Questions
Exam 6: Work and Kinetic Energy109 Questions
Exam 7: Potential Energy and Energy Conservation50 Questions
Exam 8: Momentum, Impulse, and Collisions99 Questions
Exam 9: Rotation of Rigid Bodies26 Questions
Exam 10: Dynamics of Rotational Motion49 Questions
Exam 11: Equilibrium and Elasticity50 Questions
Exam 12: Fluid Mechanics54 Questions
Exam 13: Gravitation52 Questions
Exam 14: Periodic Motion109 Questions
Exam 15: Mechanical Waves50 Questions
Exam 16: Sound and Hearing121 Questions
Exam 17: Temperature and Heat60 Questions
Exam 18: Thermal Properties of Matter41 Questions
Exam 19: The First Law of Thermodynamics55 Questions
Exam 20: The Second Law of Thermodynamics52 Questions
Exam 21: Electric Charge and Electric Field54 Questions
Exam 22: Gausss Law54 Questions
Exam 23: Electric Potential88 Questions
Exam 24: Capacitance and Dielectrics70 Questions
Exam 25: Current, Resistance, and Electromotive Force44 Questions
Exam 26: Direct-Current Circuits51 Questions
Exam 27: Magnetic Field and Magnetic Forces105 Questions
Exam 28: Sources of Magnetic Field82 Questions
Exam 29: Electromagnetic Induction51 Questions
Exam 30: Inductance88 Questions
Exam 31: Alternating Current51 Questions
Exam 32: Electromagnetic Waves Optics53 Questions
Exam 33: The Nature and Propagation of Light31 Questions
Exam 34: Geometric Optics89 Questions
Exam 35: Interference59 Questions
Select questions type
Scalar (dot) product: The angle between vector 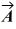 = 2.00
= 2.00  + 3.00
+ 3.00  and vector
and vector 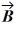 is
is 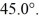 The scalar product of vectors
The scalar product of vectors 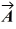 and
and 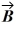 is 3.00. If the x component of vector
is 3.00. If the x component of vector 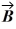 is positive, what is vector
is positive, what is vector 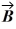 .
.
Free
(Multiple Choice)
4.7/5  (47)
(47)
Correct Answer:
B
Components: Vector 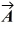 has a magnitude 5.00 and points in a direction 40.0° clockwise from the negative y axis. What are the x and y components of vector
has a magnitude 5.00 and points in a direction 40.0° clockwise from the negative y axis. What are the x and y components of vector 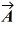 .
.
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
C
Vector (cross) product: If 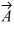 and
and 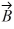 are nonzero vectors for which
are nonzero vectors for which 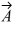 ∙
∙ 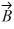 = 0, it must follow that
= 0, it must follow that
Free
(Multiple Choice)
4.9/5  (34)
(34)
Correct Answer:
C
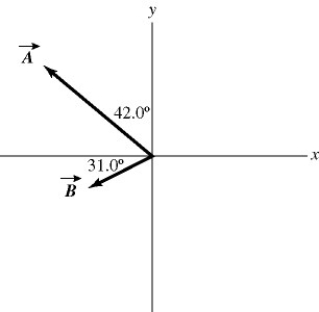
Addition and subtraction: Vectors 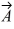 and
and 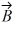 are shown in the figure. Vector
are shown in the figure. Vector 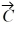 is given by
is given by 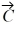 =
= 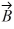 -
- 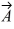 . The magnitude of vector
. The magnitude of vector  is 16.0 units, and the magnitude of vector
is 16.0 units, and the magnitude of vector 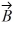 is 7.00 units. What is the magnitude of vector
is 7.00 units. What is the magnitude of vector 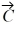 ?
? 
(Multiple Choice)
4.7/5  (36)
(36)
Addition and subtraction: Vectors 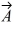 and
and 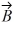 are shown in the figure. Vector
are shown in the figure. Vector 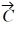 is given by
is given by 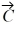 =
= 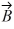 -
- 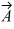 . The magnitude of vector
. The magnitude of vector 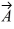 is 16.0 units, and the magnitude of vector
is 16.0 units, and the magnitude of vector 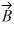 is 7.00 units. What is the angle of vector
is 7.00 units. What is the angle of vector 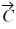 , measured counterclockwise from the +x-axis?
, measured counterclockwise from the +x-axis? 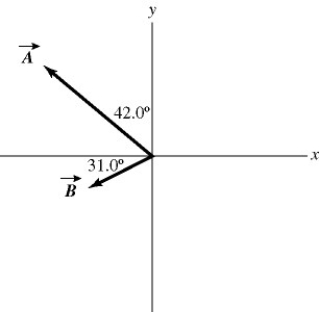
(Multiple Choice)
4.7/5  (40)
(40)
Vector (cross) product: For the vectors shown in the figure, find the magnitude and direction of  ×
×  , assuming that the quantities shown are accurate to two significant figures.
, assuming that the quantities shown are accurate to two significant figures. 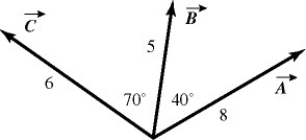
(Multiple Choice)
4.9/5  (38)
(38)
Vector (cross) product: If the magnitude of the cross product of two vectors is one-half the dot product of the same vectors, what is the angle between the two vectors?
(Short Answer)
4.7/5  (34)
(34)
Scalar (dot) product: What is the angle between the vector 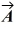 = + 3
= + 3  - 2
- 2  - 3
- 3 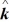 and the +y-axis?
and the +y-axis?
(Multiple Choice)
4.8/5  (35)
(35)
Vector (cross) product: What is the magnitude of the cross product of a vector of magnitude 2.00 m pointing east and a vector of magnitude 4.00 m pointing 30.0° west of north?
(Multiple Choice)
4.9/5  (34)
(34)
Scalar (dot) product: The scalar product of vector 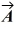 = 3.00
= 3.00  + 2.00
+ 2.00  and vector
and vector 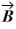 is 10.0. Which of the following vectors could be vector
is 10.0. Which of the following vectors could be vector 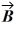 ?
?
(Multiple Choice)
4.8/5  (31)
(31)
Components: The components of vector 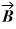 are
are 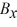 = -3.5 and
= -3.5 and 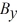 = -9.7, and the components of vector
= -9.7, and the components of vector 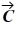 are
are 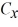 = -6 and
= -6 and 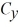 = + 8.1. What is the angle (less than 180 degrees) between vectors
= + 8.1. What is the angle (less than 180 degrees) between vectors 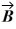 and
and 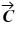 ?
?
(Multiple Choice)
4.9/5  (26)
(26)
Components: If the eastward component of vector 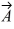 is equal to the westward component of vector
is equal to the westward component of vector 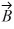 and their northward components are equal. Which one of the following statements about these two vectors is correct?
and their northward components are equal. Which one of the following statements about these two vectors is correct?
(Multiple Choice)
4.9/5  (33)
(33)
Components: Vector 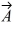 has a magnitude of 5.5 cm and points along the x-axis. Vector
has a magnitude of 5.5 cm and points along the x-axis. Vector 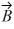 has a magnitude of 7.5 cm and points at +30° above the negative x-axis.
(a) Determine the x and y components of Vector
has a magnitude of 7.5 cm and points at +30° above the negative x-axis.
(a) Determine the x and y components of Vector 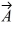 .
(b) Determine the x and y components of Vector
.
(b) Determine the x and y components of Vector 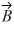 .
(c) Determine x and y components of the sum of these two vectors.
(d) Determine the magnitude and direction of the sum of these two vectors.
.
(c) Determine x and y components of the sum of these two vectors.
(d) Determine the magnitude and direction of the sum of these two vectors.
(Essay)
4.7/5  (33)
(33)
Components: A helicopter is flying horizontally with a speed of 444 m/s over a hill that slopes upward with a 2% grade (that is, the "rise" is 2% of the "run"). What is the component of the helicopter's velocity perpendicular to the sloping surface of the hill?
(Multiple Choice)
4.9/5  (30)
(30)
Scalar (dot) product: If 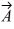 = 3
= 3  -
-  + 4
+ 4  and
and 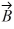 = x
= x  +
+  - 5
- 5  , find x so
, find x so 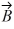 will be perpendicular to
will be perpendicular to 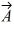 .
.
(Short Answer)
4.9/5  (32)
(32)
Components: Three forces are exerted on an object placed on a tilted floor. Forces are vectors. The three forces are directed as shown in the figure. If the forces have magnitudes 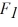 = 1.0 N,
= 1.0 N, 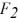 = 8.0 N and
= 8.0 N and 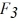 = 7.0 N, where N is the standard unit of force, what is the component of the net force
= 7.0 N, where N is the standard unit of force, what is the component of the net force 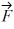 net =
net = 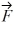 1 +
1 + 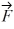 2 +
2 + 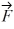 3 parallel to the floor?
3 parallel to the floor? 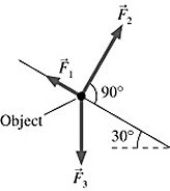
(Multiple Choice)
4.8/5  (31)
(31)
Scalar (dot) product: A rectangular box is positioned with its vertices at the following points: A = (0,0,0) C = (2,4,0) E = (0,0,3) G = (2,4,3)
B = (2,0,0) D = (0,4,0) F = (2,0,3) H = (0,4,3)
If the coordinates all have three significant figures, the angle between the line segments AG and AH is closest to:
(Multiple Choice)
5.0/5  (33)
(33)
Vector (cross) product: For the vectors shown in the figure, find the magnitude and direction of the vector product 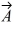 ×
× 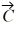 that the quantities shown are accurate to two significant figures.
that the quantities shown are accurate to two significant figures. 
(Multiple Choice)
4.8/5  (36)
(36)
Unit vectors: Vector  = -1.00
= -1.00  + -2.00
+ -2.00  and vector
and vector  = 3.00
= 3.00  + 4.00
+ 4.00  What are the magnitude and direction of vector
What are the magnitude and direction of vector 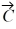 = 3.00
= 3.00 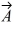 + 2.00
+ 2.00 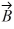 ?
?
(Multiple Choice)
4.9/5  (30)
(30)
Showing 1 - 20 of 55
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)