Deck 10: Topics From Analytic Geometry
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/15
Play
Full screen (f)
Deck 10: Topics From Analytic Geometry
1
Select the correct graph of the following equations of the hyperbola and find the center of the hyperbola.
Center: 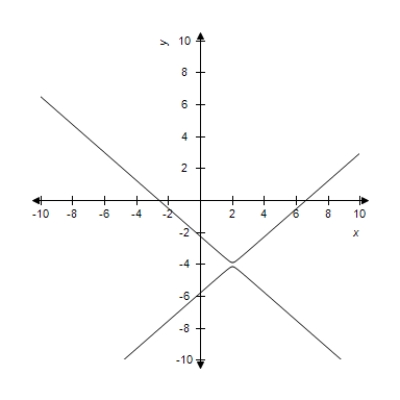

2
Find the standard form of the equation of the ellipse with the given characteristics.
Foci: ; major axis of length 10.
Foci: ; major axis of length 10.
3
Graph the hyperbola.
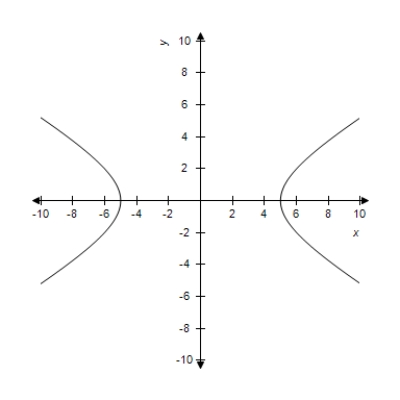

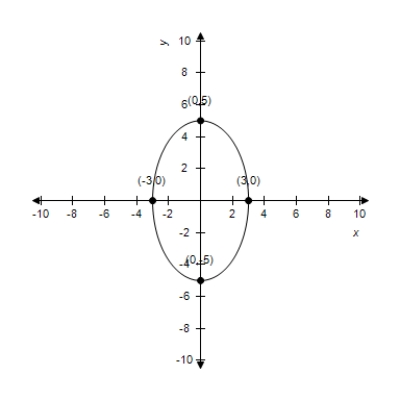
4
Find the standard form of the equation of the ellipse with the given characteristics and center at the origin.


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
5
Describe the graph of the polar equation and find the corresponding rectangular equation. Select the correct graph.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
6
Identify the conic as a circle or an ellipse then find the center.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
7
Find the standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin.
Passes through the point ; vertical axis
Passes through the point ; vertical axis

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
8
Select the polar equation of graph.
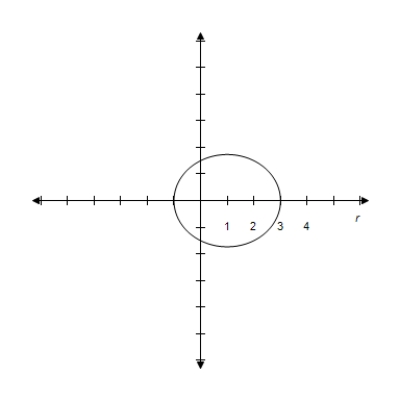


Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
9
A satellite in a 100-mile-high circular orbit around Earth has a velocity of approximately 17,500 miles per hour. If this velocity is multiplied by , the satellite will have the minimum velocity necessary to escape Earth's gravity and will follow a parabolic path with the center of Earth as the focus. (Hints: The radius of Earth is 4,000 miles.)
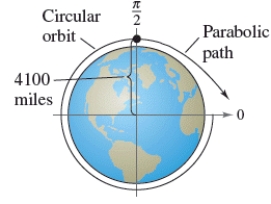 Find the distance between the surface of the Earth and the satellite when .
Find the distance between the surface of the Earth and the satellite when .
 Find the distance between the surface of the Earth and the satellite when .
Find the distance between the surface of the Earth and the satellite when .

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
10
Find a polar equation of the conic with its focus at the pole.
Conics
Vertex or vertices
Parabola
Conics
Vertex or vertices
Parabola

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
11
Graph the hyperbola.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
12
Eliminate the parameter and write the corresponding rectangular equation whose graph represents the curve.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
13
Find a set of parametric equations for the rectangular equation.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
14
Identify the conic by writing the equation in standard form.

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck
15
Find a polar equation of the conic with its focus at the pole.
Conics
Eccentricity
Directrix
Hyperbola
Conics
Eccentricity
Directrix
Hyperbola

Unlock Deck
Unlock for access to all 15 flashcards in this deck.
Unlock Deck
k this deck


