Exam 10: Topics From Analytic Geometry
Exam 1: Topics From Algebra14 Questions
Exam 2: Functions and Graphs14 Questions
Exam 3: Polynomial and Rational Functions15 Questions
Exam 4: Inverse, Exponential, and Logarithmic Functions15 Questions
Exam 5: The Trigonometric Functions15 Questions
Exam 6: Analytic Trigonometry15 Questions
Exam 7: Applications of Trigonometry15 Questions
Exam 8: Systems of Equations and Inequalities15 Questions
Exam 9: Sequences, Series, and Probability15 Questions
Exam 10: Topics From Analytic Geometry15 Questions
Exam 11: Limits of Functions15 Questions
Select questions type
Identify the conic as a circle or an ellipse then find the center.
Free
(Short Answer)
4.8/5  (36)
(36)
Correct Answer:
Ellipse
Center:
Identify the conic by writing the equation in standard form.
Free
(Short Answer)
5.0/5  (44)
(44)
Correct Answer:
; ellipse
Find a polar equation of the conic with its focus at the pole.
Conics
Eccentricity
Directrix
Hyperbola
Free
(Short Answer)
4.8/5  (40)
(40)
Correct Answer:
Find a polar equation of the conic with its focus at the pole.
Conics
Vertex or vertices
Parabola
(Short Answer)
4.8/5  (38)
(38)
Find the standard form of the equation of the parabola with the given characteristic(s) and vertex at the origin.
Passes through the point ; vertical axis
(Short Answer)
4.8/5  (33)
(33)
Describe the graph of the polar equation and find the corresponding rectangular equation. Select the correct graph.
(Short Answer)
4.8/5  (37)
(37)
A satellite in a 100-mile-high circular orbit around Earth has a velocity of approximately 17,500 miles per hour. If this velocity is multiplied by , the satellite will have the minimum velocity necessary to escape Earth's gravity and will follow a parabolic path with the center of Earth as the focus. (Hints: The radius of Earth is 4,000 miles.)
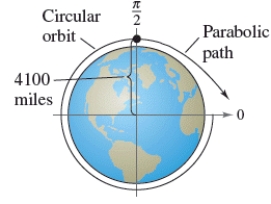 Find the distance between the surface of the Earth and the satellite when .
Find the distance between the surface of the Earth and the satellite when .
(Short Answer)
4.9/5  (35)
(35)
Eliminate the parameter and write the corresponding rectangular equation whose graph represents the curve.
(Short Answer)
4.9/5  (37)
(37)
Find the standard form of the equation of the ellipse with the given characteristics.
Foci: ; major axis of length 10.
(Short Answer)
4.8/5  (37)
(37)
Select the correct graph of the following equations of the hyperbola and find the center of the hyperbola.
(Short Answer)
4.9/5  (37)
(37)
Find a set of parametric equations for the rectangular equation.
t=3-x x=4y-3
(Short Answer)
4.9/5  (36)
(36)
Find the standard form of the equation of the ellipse with the given characteristics and center at the origin.
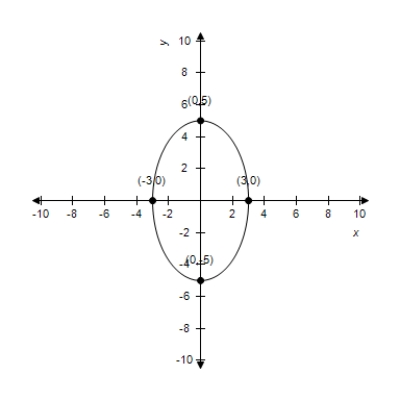
(Short Answer)
4.8/5  (26)
(26)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)