Deck 9: Linear Transformations
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/60
Play
Full screen (f)
Deck 9: Linear Transformations
1
Let 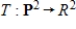 be a linear transformation satisfying
be a linear transformation satisfying 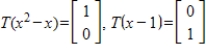 .
.
Find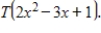
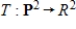 be a linear transformation satisfying
be a linear transformation satisfying 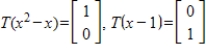 .
.Find
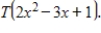
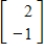
2
Let  be a linear transformation satisfying
be a linear transformation satisfying 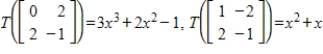 .Find
.Find 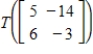 .
.
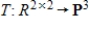 be a linear transformation satisfying
be a linear transformation satisfying  .Find
.Find 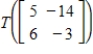 .
.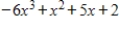
3
Determine whether the function 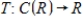 is a linear transformation, where
is a linear transformation, where 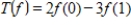 .
.
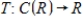 is a linear transformation, where
is a linear transformation, where 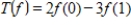 .
.T is a linear transformation.
4
Determine whether the function 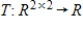 is a linear transformation, where
is a linear transformation, where 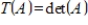 .
.
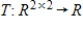 is a linear transformation, where
is a linear transformation, where 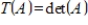 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
5
Determine whether the function 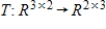 is a linear transformation, where
is a linear transformation, where 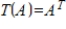 .
.
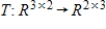 is a linear transformation, where
is a linear transformation, where 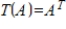 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
6
Determine the kernel and range of the linear transformation 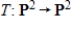 given by
given by
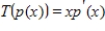 .
.
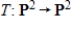 given by
given by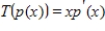 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
7
Determine if the linear transformation 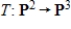 is one-to-one and/or onto.
is one-to-one and/or onto.
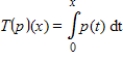
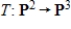 is one-to-one and/or onto.
is one-to-one and/or onto.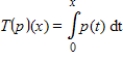

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
8
Let Q be an 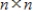 invertible matrix, and let P be an
invertible matrix, and let P be an 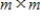 invertible matrix. Determine whether the function
invertible matrix. Determine whether the function 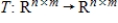 is a linear transformation, where
is a linear transformation, where 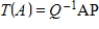 , and if so, determine if T is one-to-one and/or onto.
, and if so, determine if T is one-to-one and/or onto.
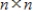 invertible matrix, and let P be an
invertible matrix, and let P be an 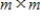 invertible matrix. Determine whether the function
invertible matrix. Determine whether the function 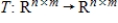 is a linear transformation, where
is a linear transformation, where 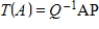 , and if so, determine if T is one-to-one and/or onto.
, and if so, determine if T is one-to-one and/or onto.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
9
If S is a nonzero subspace of 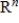 , determine whether the function
, determine whether the function 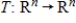 is a linear transformation, where
is a linear transformation, where 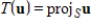 , and if so, determine
, and if so, determine 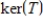 .
.
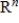 , determine whether the function
, determine whether the function 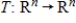 is a linear transformation, where
is a linear transformation, where 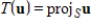 , and if so, determine
, and if so, determine 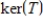 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
10
If 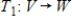 and
and 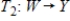 are linear transformations, then the composition
are linear transformations, then the composition 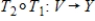 is a linear transformation.
is a linear transformation.
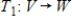 and
and 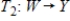 are linear transformations, then the composition
are linear transformations, then the composition 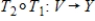 is a linear transformation.
is a linear transformation.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
11
Suppose B is an 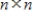 invertible matrix. The function
invertible matrix. The function 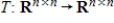 defined by
defined by 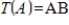 is a one-to-one and onto linear transformation.
is a one-to-one and onto linear transformation.
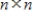 invertible matrix. The function
invertible matrix. The function 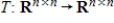 defined by
defined by 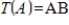 is a one-to-one and onto linear transformation.
is a one-to-one and onto linear transformation.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
12
The function 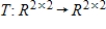 defined by
defined by 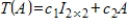 , where
, where 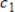 and
and  are nonzero scalars, is a linear transformation.
are nonzero scalars, is a linear transformation.
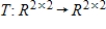 defined by
defined by 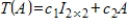 , where
, where 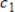 and
and  are nonzero scalars, is a linear transformation.
are nonzero scalars, is a linear transformation.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
13
Suppose 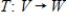 is a linear transformation and
is a linear transformation and 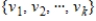 is a set of vectors in V. If
is a set of vectors in V. If 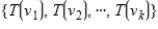 is a linearly dependent set, then so is
is a linearly dependent set, then so is 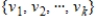 .
.
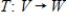 is a linear transformation and
is a linear transformation and 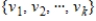 is a set of vectors in V. If
is a set of vectors in V. If 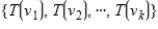 is a linearly dependent set, then so is
is a linearly dependent set, then so is 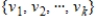 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
14
If 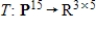 is an onto linear transformation, then T is one-to-one.
is an onto linear transformation, then T is one-to-one.
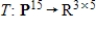 is an onto linear transformation, then T is one-to-one.
is an onto linear transformation, then T is one-to-one.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
15
Suppose 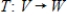 is a linear transformation that is not one-to-one, and is not the trivial transformation, that is,
is a linear transformation that is not one-to-one, and is not the trivial transformation, that is, 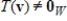 for some v in V. Then
for some v in V. Then 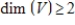 .
.
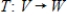 is a linear transformation that is not one-to-one, and is not the trivial transformation, that is,
is a linear transformation that is not one-to-one, and is not the trivial transformation, that is, 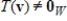 for some v in V. Then
for some v in V. Then 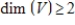 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
16
Suppose S is a proper subspace of 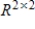 . Can S be isomorphic to
. Can S be isomorphic to 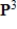 ?
?
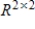 . Can S be isomorphic to
. Can S be isomorphic to 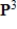 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
17
Suppose S is a proper subspace of 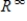 . Can S be isomorphic to
. Can S be isomorphic to 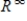 ?
?
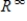 . Can S be isomorphic to
. Can S be isomorphic to 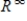 ?
?
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
18
Determine if the linear transformation 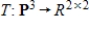 is an isomorphism.
is an isomorphism.
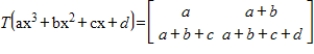
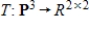 is an isomorphism.
is an isomorphism.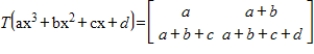

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
19
Determine if the linear transformation 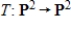 is an isomorphism.
is an isomorphism.
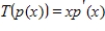
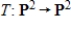 is an isomorphism.
is an isomorphism.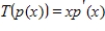

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
20
Find 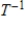 for the isomorphism
for the isomorphism 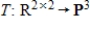 , where
, where 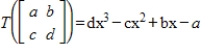 .
.
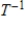 for the isomorphism
for the isomorphism 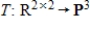 , where
, where 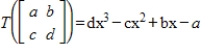 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
21
Suppose A and B are 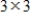 invertible matrices. Find
invertible matrices. Find 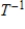 for the isomorphism
for the isomorphism 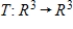 , where
, where 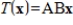 .
.
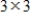 invertible matrices. Find
invertible matrices. Find 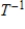 for the isomorphism
for the isomorphism 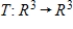 , where
, where 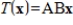 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
22
Find 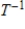 for the isomorphism
for the isomorphism 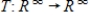 , where
, where
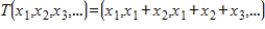
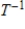 for the isomorphism
for the isomorphism 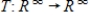 , where
, where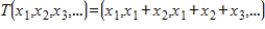

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
23
Suppose 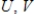 are
are 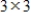 orthogonal matrices, and let
orthogonal matrices, and let 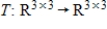 be defined by
be defined by 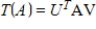 . Verify that
. Verify that 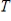 is a linear transformation, determine if
is a linear transformation, determine if 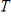 is an isomorphism, and if so, find
is an isomorphism, and if so, find 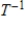 .
.
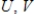 are
are 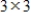 orthogonal matrices, and let
orthogonal matrices, and let 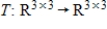 be defined by
be defined by 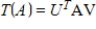 . Verify that
. Verify that 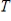 is a linear transformation, determine if
is a linear transformation, determine if 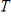 is an isomorphism, and if so, find
is an isomorphism, and if so, find 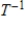 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
24
Let 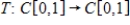 be defined by
be defined by 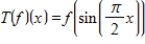 . Verify that
. Verify that 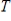 is a linear transformation, determine if
is a linear transformation, determine if 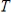 is an isomorphism, and if so, find
is an isomorphism, and if so, find 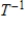 .
.
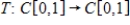 be defined by
be defined by 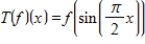 . Verify that
. Verify that 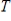 is a linear transformation, determine if
is a linear transformation, determine if 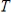 is an isomorphism, and if so, find
is an isomorphism, and if so, find 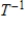 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
25
Find 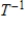 for the isomorphism
for the isomorphism 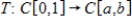 , where
, where 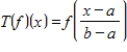 , for
, for 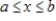 .
.
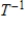 for the isomorphism
for the isomorphism 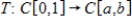 , where
, where 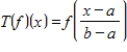 , for
, for 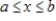 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
26
If 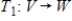 and
and 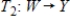 are isomorphisms, then the composition
are isomorphisms, then the composition 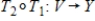 is an isomorphism.
is an isomorphism.
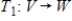 and
and 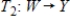 are isomorphisms, then the composition
are isomorphisms, then the composition 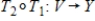 is an isomorphism.
is an isomorphism.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
27
If 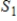 and
and 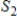 are isomorphic subspaces of a vector space V then
are isomorphic subspaces of a vector space V then 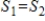 .
.
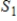 and
and 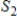 are isomorphic subspaces of a vector space V then
are isomorphic subspaces of a vector space V then 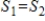 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
28
R is isomorphic to the subspace S of 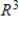 defined by
defined by 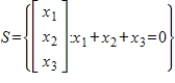 .
.
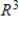 defined by
defined by 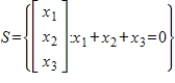 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
29
The subspace S of 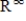 of all sequences that are eventually zero is isomorphic to
of all sequences that are eventually zero is isomorphic to  .
.
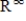 of all sequences that are eventually zero is isomorphic to
of all sequences that are eventually zero is isomorphic to  .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
30
The vector spaces 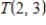 and
and 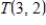 are isomorphic. (Recall that
are isomorphic. (Recall that 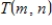 denotes the vector space of all linear transformations from
denotes the vector space of all linear transformations from 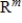 into
into 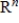
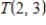 and
and 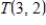 are isomorphic. (Recall that
are isomorphic. (Recall that 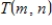 denotes the vector space of all linear transformations from
denotes the vector space of all linear transformations from 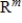 into
into 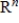

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
31
Find v given the coordinate vector 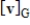 with respect to the basis G.
with respect to the basis G.
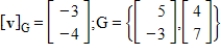
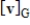 with respect to the basis G.
with respect to the basis G.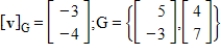

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
32
Find v given the coordinate vector 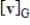 with respect to the basis G.
with respect to the basis G.
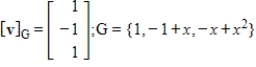
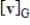 with respect to the basis G.
with respect to the basis G.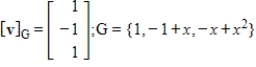

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
33
Find the coordinate vector of v with respect to the basis G. 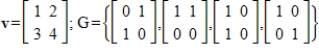
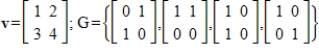

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
34
Find the coordinate vector of v with respect to the basis G. 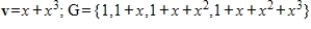
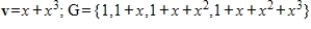

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
35
Suppose A is the matrix of the linear transformation 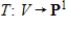 with respect to bases G and Q, respectively. Find
with respect to bases G and Q, respectively. Find 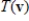 for the given
for the given 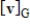 .
.
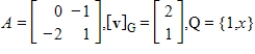
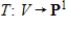 with respect to bases G and Q, respectively. Find
with respect to bases G and Q, respectively. Find 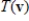 for the given
for the given 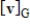 .
.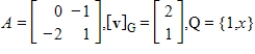

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
36
Suppose A is the matrix of the linear transformation 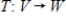 with respect to bases G and Q, respectively. Find
with respect to bases G and Q, respectively. Find 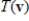 for the given
for the given 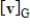 .
.
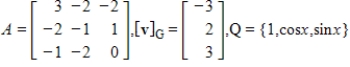
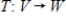 with respect to bases G and Q, respectively. Find
with respect to bases G and Q, respectively. Find 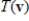 for the given
for the given 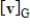 .
.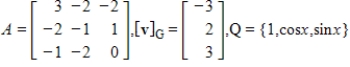

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
37
Find the matrix A of the linear transformation 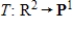 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.
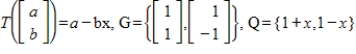
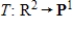 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.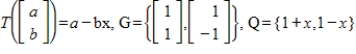

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
38
Find the matrix A of the linear transformation 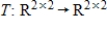 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.
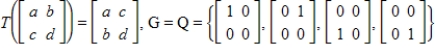
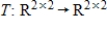 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.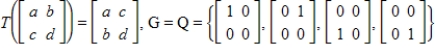

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
39
Let 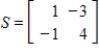 . Find the matrix A of the linear transformation
. Find the matrix A of the linear transformation 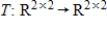 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.
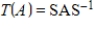 ,
, 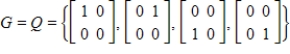
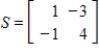 . Find the matrix A of the linear transformation
. Find the matrix A of the linear transformation 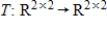 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.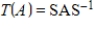 ,
, 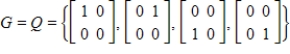

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
40
Suppose that 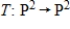 has matrix
has matrix 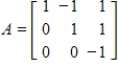 with respect to the basis
with respect to the basis 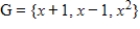 for the domain and
for the domain and 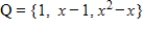 for the codomain. Use the inverse of
for the codomain. Use the inverse of 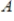 to find
to find 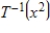 .
.
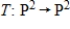 has matrix
has matrix 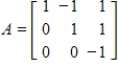 with respect to the basis
with respect to the basis 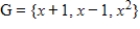 for the domain and
for the domain and 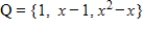 for the codomain. Use the inverse of
for the codomain. Use the inverse of 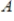 to find
to find 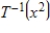 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
41
If 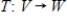 has matrix
has matrix 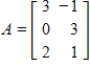 with respect to bases
with respect to bases 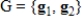 for the domain and
for the domain and 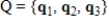 for the codomain, then the matrix of T with respect to the bases
for the codomain, then the matrix of T with respect to the bases 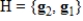 and
and 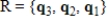 is
is 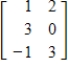 .
.
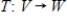 has matrix
has matrix 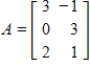 with respect to bases
with respect to bases 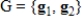 for the domain and
for the domain and 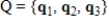 for the codomain, then the matrix of T with respect to the bases
for the codomain, then the matrix of T with respect to the bases 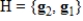 and
and 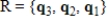 is
is 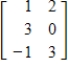 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
42
If V is a finite-dimensional vector space, then the matrix A of a linear transformation 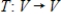 is invertible if and only if T is one-to-one.
is invertible if and only if T is one-to-one.
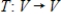 is invertible if and only if T is one-to-one.
is invertible if and only if T is one-to-one.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
43
Suppose V and W are finite dimensional vector spaces, and 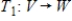 and
and 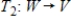 are linear transformations such that
are linear transformations such that 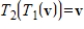 for every v in V and
for every v in V and 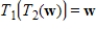 for every w in W. If the matrices
for every w in W. If the matrices 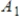 ,
, 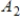 represent
represent 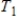 ,
, 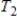 respectively (with respect to the same bases for V and W), then
respectively (with respect to the same bases for V and W), then 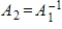 .
.
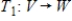 and
and 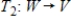 are linear transformations such that
are linear transformations such that 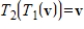 for every v in V and
for every v in V and 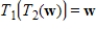 for every w in W. If the matrices
for every w in W. If the matrices 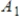 ,
, 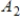 represent
represent 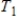 ,
, 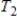 respectively (with respect to the same bases for V and W), then
respectively (with respect to the same bases for V and W), then 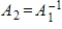 .
.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
44
If 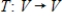 is a linear transformation, with V a vector space having basis
is a linear transformation, with V a vector space having basis 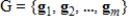 , and if
, and if 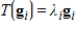 for all i, where
for all i, where 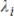 is a scalar, then the matrix of T is diagonal, where G is the basis used for both the domain and codomain.
is a scalar, then the matrix of T is diagonal, where G is the basis used for both the domain and codomain.
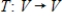 is a linear transformation, with V a vector space having basis
is a linear transformation, with V a vector space having basis 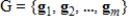 , and if
, and if 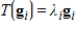 for all i, where
for all i, where 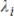 is a scalar, then the matrix of T is diagonal, where G is the basis used for both the domain and codomain.
is a scalar, then the matrix of T is diagonal, where G is the basis used for both the domain and codomain.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
45
Let V be a vector space with basis 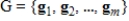 , and let
, and let 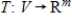 be the linear transformation
be the linear transformation 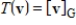 . Then T is an isomorphism, and the matrix of T with respect to G and the standard basis is the
. Then T is an isomorphism, and the matrix of T with respect to G and the standard basis is the 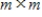 identity matrix.
identity matrix.
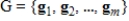 , and let
, and let 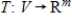 be the linear transformation
be the linear transformation 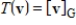 . Then T is an isomorphism, and the matrix of T with respect to G and the standard basis is the
. Then T is an isomorphism, and the matrix of T with respect to G and the standard basis is the 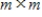 identity matrix.
identity matrix.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
46
Find the change of basis matrix from G to H.
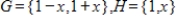
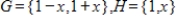

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
47
Find the change of basis matrix from G to H.
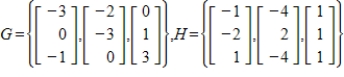
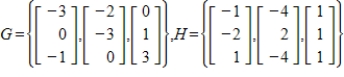

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
48
Suppose B is the matrix of 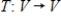 with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G.
with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G. 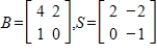
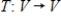 with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G.
with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G. 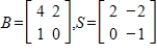

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
49
Suppose B is the matrix of 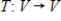 with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G.
with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G. 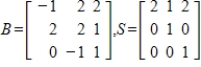
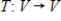 with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G.
with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G. 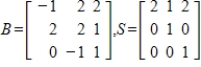

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
50
Suppose B is the matrix of 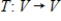 with respect to the basis H. Find the matrix A of T with respect to the basis G.
with respect to the basis H. Find the matrix A of T with respect to the basis G. 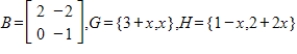
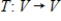 with respect to the basis H. Find the matrix A of T with respect to the basis G.
with respect to the basis H. Find the matrix A of T with respect to the basis G. 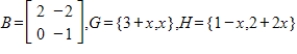

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
51
Suppose B is the matrix of 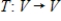 with respect to the basis H. Find the matrix A of T with respect to the basis G.
with respect to the basis H. Find the matrix A of T with respect to the basis G. 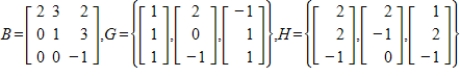
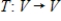 with respect to the basis H. Find the matrix A of T with respect to the basis G.
with respect to the basis H. Find the matrix A of T with respect to the basis G. 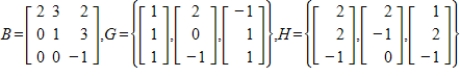

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
52
Determine if A and B are similar matrices.
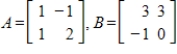
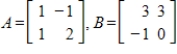

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
53
Determine if A and B are similar matrices.
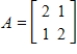 ,
, 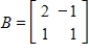
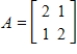 ,
, 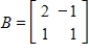

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
54
Determine if A and B are similar matrices.
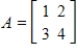 ,
,
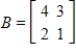
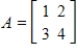 ,
,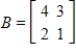

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
55
Determine if A and B are similar matrices.
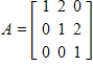 ,
,
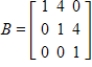
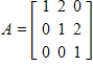 ,
,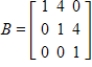

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
56
If A and B are similar matrices and B and C are similar matrices, then A and C are similar matrices.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
57
Every change of basis matrix is invertible.

Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
58
If S is a change of basis matrix from basis G to basis H, then 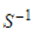 is a change of basis matrix from H to
is a change of basis matrix from H to
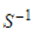 is a change of basis matrix from H to
is a change of basis matrix from H to
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
59
If A is an 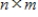 matrix, then
matrix, then 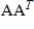 is similar to an
is similar to an 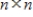 diagonal matrix.
diagonal matrix.
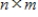 matrix, then
matrix, then 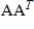 is similar to an
is similar to an 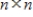 diagonal matrix.
diagonal matrix.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck
60
If A, B, C, and D are 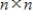 matrices such that A is similar to B and C is similar to D, then AC is similar to BD.
matrices such that A is similar to B and C is similar to D, then AC is similar to BD.
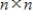 matrices such that A is similar to B and C is similar to D, then AC is similar to BD.
matrices such that A is similar to B and C is similar to D, then AC is similar to BD.
Unlock Deck
Unlock for access to all 60 flashcards in this deck.
Unlock Deck
k this deck


