Exam 9: Linear Transformations
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
Determine if A and B are similar matrices.
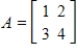 ,
,
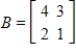
Free
(Short Answer)
4.8/5  (33)
(33)
Correct Answer:
A and B are similar matrices.
Find v given the coordinate vector 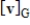 with respect to the basis G.
with respect to the basis G.
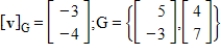
Free
(Essay)
4.9/5  (34)
(34)
Correct Answer:
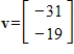
Determine whether the function 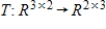 is a linear transformation, where
is a linear transformation, where 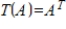 .
.
Free
(Short Answer)
4.9/5  (32)
(32)
Correct Answer:
T is a linear transformation.
If 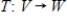 has matrix
has matrix 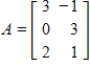 with respect to bases
with respect to bases 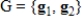 for the domain and
for the domain and 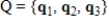 for the codomain, then the matrix of T with respect to the bases
for the codomain, then the matrix of T with respect to the bases 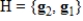 and
and 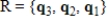 is
is 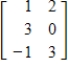 .
.
(True/False)
4.9/5  (29)
(29)
Let 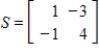 . Find the matrix A of the linear transformation
. Find the matrix A of the linear transformation 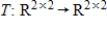 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.
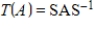 ,
, 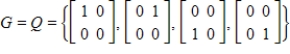
(Essay)
4.8/5  (41)
(41)
Suppose that 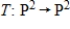 has matrix
has matrix 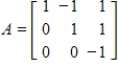 with respect to the basis
with respect to the basis 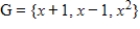 for the domain and
for the domain and 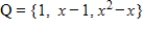 for the codomain. Use the inverse of
for the codomain. Use the inverse of  to find
to find 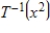 .
.
(Essay)
4.9/5  (30)
(30)
Suppose A is the matrix of the linear transformation 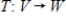 with respect to bases G and Q, respectively. Find
with respect to bases G and Q, respectively. Find 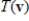 for the given
for the given 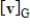 .
.
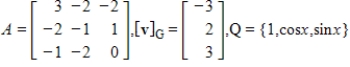
(Essay)
5.0/5  (36)
(36)
If S is a change of basis matrix from basis G to basis H, then 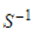 is a change of basis matrix from H to
is a change of basis matrix from H to
(True/False)
4.9/5  (28)
(28)
Find the matrix A of the linear transformation 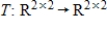 with respect to bases G and Q, respectively.
with respect to bases G and Q, respectively.
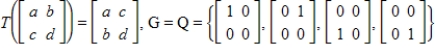
(Essay)
4.7/5  (39)
(39)
Suppose B is the matrix of 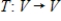 with respect to the basis H. Find the matrix A of T with respect to the basis G.
with respect to the basis H. Find the matrix A of T with respect to the basis G. 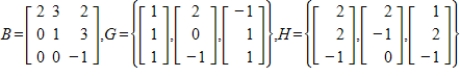
(Essay)
5.0/5  (31)
(31)
Suppose V and W are finite dimensional vector spaces, and 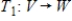 and
and 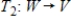 are linear transformations such that
are linear transformations such that 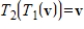 for every v in V and
for every v in V and 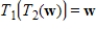 for every w in W. If the matrices
for every w in W. If the matrices  ,
,  represent
represent  ,
, 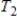 respectively (with respect to the same bases for V and W), then
respectively (with respect to the same bases for V and W), then 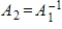 .
.
(True/False)
4.8/5  (29)
(29)
Suppose B is an 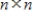 invertible matrix. The function
invertible matrix. The function 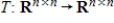 defined by
defined by 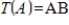 is a one-to-one and onto linear transformation.
is a one-to-one and onto linear transformation.
(True/False)
4.9/5  (45)
(45)
Suppose 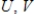 are
are 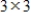 orthogonal matrices, and let
orthogonal matrices, and let 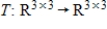 be defined by
be defined by 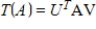 . Verify that
. Verify that 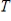 is a linear transformation, determine if
is a linear transformation, determine if 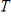 is an isomorphism, and if so, find
is an isomorphism, and if so, find 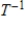 .
.
(Essay)
4.9/5  (40)
(40)
Suppose 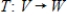 is a linear transformation that is not one-to-one, and is not the trivial transformation, that is,
is a linear transformation that is not one-to-one, and is not the trivial transformation, that is, 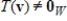 for some v in V. Then
for some v in V. Then 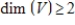 .
.
(True/False)
4.9/5  (27)
(27)
Suppose B is the matrix of 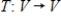 with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G.
with respect to a basis H, and S is the change of basis matrix from a basis G to H. Find the matrix A of T with respect to G. 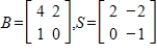
(Essay)
4.8/5  (32)
(32)
Showing 1 - 20 of 60
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)