Deck 7: Vector Spaces
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question
Question

Unlock Deck
Sign up to unlock the cards in this deck!
Unlock Deck
Unlock Deck
1/45
Play
Full screen (f)
Deck 7: Vector Spaces
1
Let V be the set of all vectors 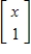 , where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.
, where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.
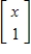 , where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.
, where x is in R. Using the usual rules for vector addition and scalar multiplication in R2, determine if V is a vector space, and if not explain why.V is not a vector space, since it contains no zero vector.
2
Let V be the set of all functions f : R  R such that
R such that 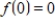 . Using the usual rules for vector addition and scalar multiplication of functions, determine if V is a vector space, and if not explain why.
. Using the usual rules for vector addition and scalar multiplication of functions, determine if V is a vector space, and if not explain why.
 R such that
R such that 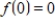 . Using the usual rules for vector addition and scalar multiplication of functions, determine if V is a vector space, and if not explain why.
. Using the usual rules for vector addition and scalar multiplication of functions, determine if V is a vector space, and if not explain why.V is a vector space.
3
In the vector space 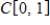 , let S be the set of all functions f such that
, let S be the set of all functions f such that 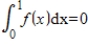 . Determine if S is a subspace, and if not explain why.
. Determine if S is a subspace, and if not explain why.
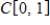 , let S be the set of all functions f such that
, let S be the set of all functions f such that 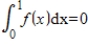 . Determine if S is a subspace, and if not explain why.
. Determine if S is a subspace, and if not explain why.S is a subspace.
4
In the vector space V of all differentiable functions 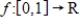 , let S be the set of all functions f such that
, let S be the set of all functions f such that 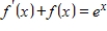 . Determine if S is a subspace of V, and if not explain why.
. Determine if S is a subspace of V, and if not explain why.
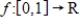 , let S be the set of all functions f such that
, let S be the set of all functions f such that 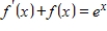 . Determine if S is a subspace of V, and if not explain why.
. Determine if S is a subspace of V, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
5
In the vector space 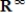 , let S be the set of all sequences
, let S be the set of all sequences 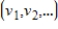 such that
such that 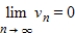 . Determine if S is a subspace of
. Determine if S is a subspace of 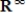 , and if not explain why.
, and if not explain why.
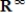 , let S be the set of all sequences
, let S be the set of all sequences 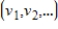 such that
such that 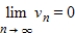 . Determine if S is a subspace of
. Determine if S is a subspace of 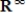 , and if not explain why.
, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
6
In the vector space 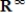 , let S be the set of all sequences
, let S be the set of all sequences 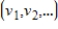 such that there exists some
such that there exists some 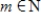 such that
such that 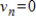 for all
for all 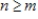 (all eventually-zero sequences). Determine if S is a subspace of
(all eventually-zero sequences). Determine if S is a subspace of 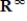 , and if not explain why.
, and if not explain why.
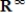 , let S be the set of all sequences
, let S be the set of all sequences 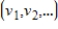 such that there exists some
such that there exists some 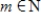 such that
such that 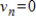 for all
for all 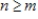 (all eventually-zero sequences). Determine if S is a subspace of
(all eventually-zero sequences). Determine if S is a subspace of 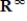 , and if not explain why.
, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
7
In the vector space 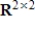 , let S be the set of matrices A such that
, let S be the set of matrices A such that 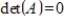 . Determine if S is a subspace of
. Determine if S is a subspace of 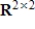 , and if not explain why.
, and if not explain why.
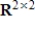 , let S be the set of matrices A such that
, let S be the set of matrices A such that 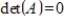 . Determine if S is a subspace of
. Determine if S is a subspace of 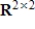 , and if not explain why.
, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
8
In the vector space 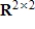 , let S be the set of matrices A such that
, let S be the set of matrices A such that 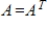 . Determine if S is a subspace of
. Determine if S is a subspace of 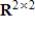 , and if not explain why.
, and if not explain why.
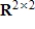 , let S be the set of matrices A such that
, let S be the set of matrices A such that 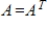 . Determine if S is a subspace of
. Determine if S is a subspace of 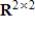 , and if not explain why.
, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
9
In the vector space 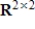 , let S be the set of matrices A such that A is not invertible. Determine if S is a subspace of
, let S be the set of matrices A such that A is not invertible. Determine if S is a subspace of 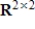 , and if not explain why.
, and if not explain why.
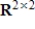 , let S be the set of matrices A such that A is not invertible. Determine if S is a subspace of
, let S be the set of matrices A such that A is not invertible. Determine if S is a subspace of 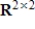 , and if not explain why.
, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
10
Let V be a vector space with vector addition 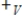 and scalar multiplication
and scalar multiplication 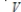 , and let W be a vector space with vector addition
, and let W be a vector space with vector addition 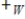 and scalar multiplication
and scalar multiplication 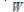 . Define
. Define 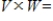
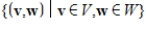 , with addition
, with addition 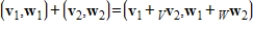 and scalar multiplication
and scalar multiplication 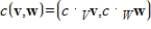 . Determine if
. Determine if 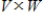 is a vector space, and if not explain why.
is a vector space, and if not explain why.
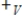 and scalar multiplication
and scalar multiplication 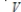 , and let W be a vector space with vector addition
, and let W be a vector space with vector addition 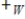 and scalar multiplication
and scalar multiplication 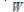 . Define
. Define 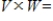
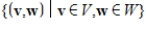 , with addition
, with addition 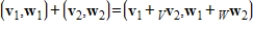 and scalar multiplication
and scalar multiplication 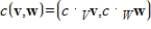 . Determine if
. Determine if 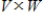 is a vector space, and if not explain why.
is a vector space, and if not explain why.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
11
The set V of all nonnegative real numbers, using the usual rules for vector addition and scalar multiplication in R, is a vector space.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
12
If V is a vector space and 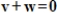 for all vectors v and w in V, then V consists of only the zero vector.
for all vectors v and w in V, then V consists of only the zero vector.
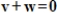 for all vectors v and w in V, then V consists of only the zero vector.
for all vectors v and w in V, then V consists of only the zero vector.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
13
For every 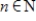 , the set
, the set 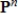 of all polynomials of degree less than or equal to n is a subspace of
of all polynomials of degree less than or equal to n is a subspace of 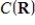 .
.
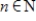 , the set
, the set 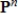 of all polynomials of degree less than or equal to n is a subspace of
of all polynomials of degree less than or equal to n is a subspace of 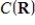 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
14
If 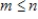 then the polynomial space
then the polynomial space 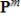 is a subspace of
is a subspace of 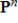 .
.
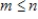 then the polynomial space
then the polynomial space 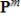 is a subspace of
is a subspace of 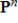 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
15
If S is a subspace of the polynomial space 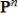 , then
, then 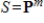 for some m with
for some m with 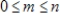 .
.
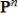 , then
, then 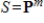 for some m with
for some m with 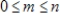 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
16
Determine if 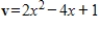 is in the subspace of
is in the subspace of 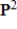 given by
given by 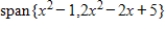 .
.
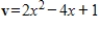 is in the subspace of
is in the subspace of 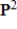 given by
given by 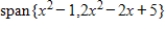 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
17
Determine if 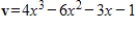 is in the subspace of
is in the subspace of 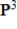 given by
given by 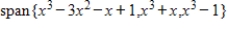 .
.
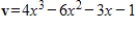 is in the subspace of
is in the subspace of 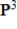 given by
given by 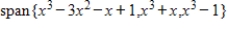 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
18
Determine if 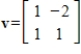 is in the subspace of
is in the subspace of  given by
given by 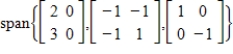 .
.
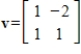 is in the subspace of
is in the subspace of 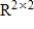 given by
given by 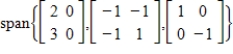 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
19
Determine if 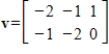 is in the subspace of
is in the subspace of  given by
given by 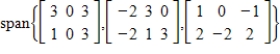 .
.
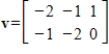 is in the subspace of
is in the subspace of 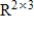 given by
given by 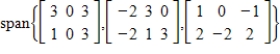 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
20
Determine if 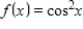 is in the subspace of
is in the subspace of 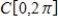 given by
given by 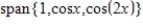 .
.
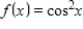 is in the subspace of
is in the subspace of 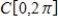 given by
given by 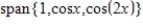 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
21
Determine if the set of vectors 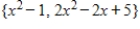 is linearly independent in
is linearly independent in 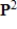 .
.
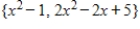 is linearly independent in
is linearly independent in 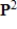 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
22
Determine if the set of vectors 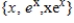 is linearly independent in
is linearly independent in 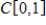 .
.
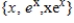 is linearly independent in
is linearly independent in 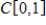 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
23
Determine if the set of vectors 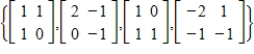 is linearly independent in
is linearly independent in 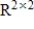 .
.
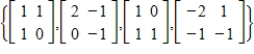 is linearly independent in
is linearly independent in 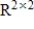 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
24
Determine if the set of vectors 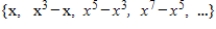 is linearly independent in P.
is linearly independent in P.
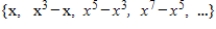 is linearly independent in P.
is linearly independent in P.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
25
Determine if the set of vectors 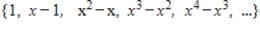 spans P.
spans P.
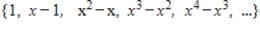 spans P.
spans P.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
26
If S spans a subspace of a vector space V, then S is linearly independent in V.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
27
If S is a linearly independent subset of a vector space V, then S spans V.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
28
If S is a linearly independent subset of a vector space V, but S does not span V, then there exists a vector v in V such that the set 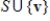 is also linearly independent.
is also linearly independent.
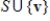 is also linearly independent.
is also linearly independent.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
29
If S spans a vector space V, but S is not linearly independent in V, then there exists a vector v in S such that the set difference 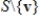 also spans V.
also spans V.
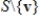 also spans V.
also spans V.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
30
Every vector space V has a finite set S which both spans V and is linearly independent in V.

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
31
Determine if the set 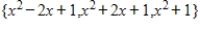 is a basis for the vector space
is a basis for the vector space 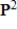 .
.
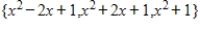 is a basis for the vector space
is a basis for the vector space 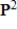 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
32
Determine if the given set is a basis for the vector space 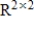 .
.
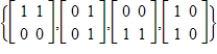
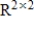 .
.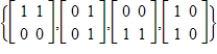

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
33
Determine if the given set is a basis for the vector space  .
.
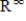 .
.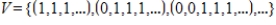

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
34
Find a basis for the subspace S of 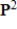 consisting of all polynomials p satisfying
consisting of all polynomials p satisfying 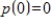 .
.
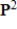 consisting of all polynomials p satisfying
consisting of all polynomials p satisfying 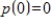 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
35
Find a basis for the subspace S of 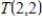 consisting of all linear transformations
consisting of all linear transformations 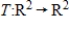 such that
such that
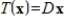 for some
for some 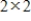 diagonal matrix D.
diagonal matrix D.
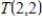 consisting of all linear transformations
consisting of all linear transformations 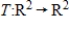 such that
such that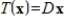 for some
for some 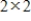 diagonal matrix D.
diagonal matrix D.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
36
Find a basis for the subspace S of P consisting of all even polynomials, that is, all polynomials p satisfying 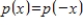 for all x.
for all x.
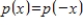 for all x.
for all x.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
37
Determine the dimension of the subspace S of 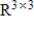 consisting of all symmetric matrices.
consisting of all symmetric matrices.
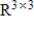 consisting of all symmetric matrices.
consisting of all symmetric matrices.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
38
Determine the dimension of the subspace S of 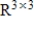 consisting of all matrices whose trace is 0.
consisting of all matrices whose trace is 0.
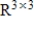 consisting of all matrices whose trace is 0.
consisting of all matrices whose trace is 0.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
39
Determine the dimension of the subspace S of 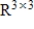 consisting of all matrices A such that
consisting of all matrices A such that
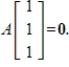
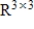 consisting of all matrices A such that
consisting of all matrices A such that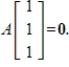

Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
40
Determine the dimension of the subspace S of 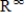 consisting of all sequences
consisting of all sequences 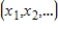 such that the series
such that the series 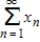 is convergent and satisfies
is convergent and satisfies 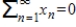 .
.
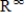 consisting of all sequences
consisting of all sequences 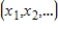 such that the series
such that the series 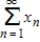 is convergent and satisfies
is convergent and satisfies 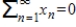 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
41
If 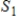 and
and 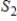 are subspaces of a vector space V and
are subspaces of a vector space V and 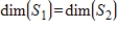 , then
, then 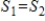 .
.
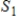 and
and 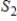 are subspaces of a vector space V and
are subspaces of a vector space V and 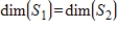 , then
, then 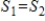 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
42
If 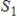 and
and 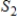 are infinite-dimensional subspaces of a vector space V, then
are infinite-dimensional subspaces of a vector space V, then 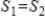 .
.
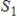 and
and 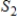 are infinite-dimensional subspaces of a vector space V, then
are infinite-dimensional subspaces of a vector space V, then 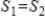 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
43
If 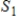 and
and 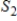 are infinite-dimensional subspaces of a vector space V, then
are infinite-dimensional subspaces of a vector space V, then 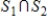 is an infinite-dimensional subspace of V.
is an infinite-dimensional subspace of V.
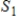 and
and 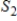 are infinite-dimensional subspaces of a vector space V, then
are infinite-dimensional subspaces of a vector space V, then 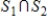 is an infinite-dimensional subspace of V.
is an infinite-dimensional subspace of V.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
44
If every finite set S in a vector space V fails to span V, then 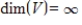 .
.
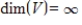 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck
45
If every infinite set S in a vector space V is linearly dependent, then 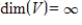 .
.
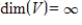 .
.
Unlock Deck
Unlock for access to all 45 flashcards in this deck.
Unlock Deck
k this deck


